Transformation of dissimilarities in community data

1. Introduction

Some dissimilarity coefficients that are popular in community ecology, such as the percentage difference (alias Bray-Curtis), have the drawback of being a non-Euclidean (dissimilarity matrices do not allow a representation in a Cartesian space), or even semi-metric (i.e. triangle inequality is not ensured). In order to use these coefficients in multivariate analyses that require these properties a transformation of the original space will normally be in order. In this section, we compare different alternatives and provide some recommendations on this issue.

library(ecotraj)

## Loading required package: Rcpp

2. Effect of square root on a simple directional trajectory

Here, we use an example of a single synthetic community to illustrate the effect of square root transformation on a community trajectory. We begin by defining the species data of the trajectory itself. The dataset consists of four rows (i.e. surveys) and four columns (species). The dynamics in this example consist in an constant increase in the number of individuals of the first species and a corresponding decrease of the others, while keeping a total abundance of 100 individuals:

sites = rep(1,4)
surveys=1:4
spdata = rbind(c(35,30,20,15),
               c(50,25,15,10),
               c(65,20,10,5),
               c(80,15,5,0))

We now use function vegdist from package vegan to calculate the Bray-Curtis coefficient:

D = vegan::vegdist(spdata, "bray")
is.metric(D)

## [1] TRUE

##      1    2    3
## 2 0.15          
## 3 0.30 0.15     
## 4 0.45 0.30 0.15

This dissimilarity matrix is a metric, so one would not need any transformation for CTA. However, it is a good example to illustrate the effect of the square root transformation.

If we draw the resemblance space corresponding to this dissimilarity matrix we see a straight trajectory:

trajectoryPCoA(D,sites,surveys, survey.labels = T)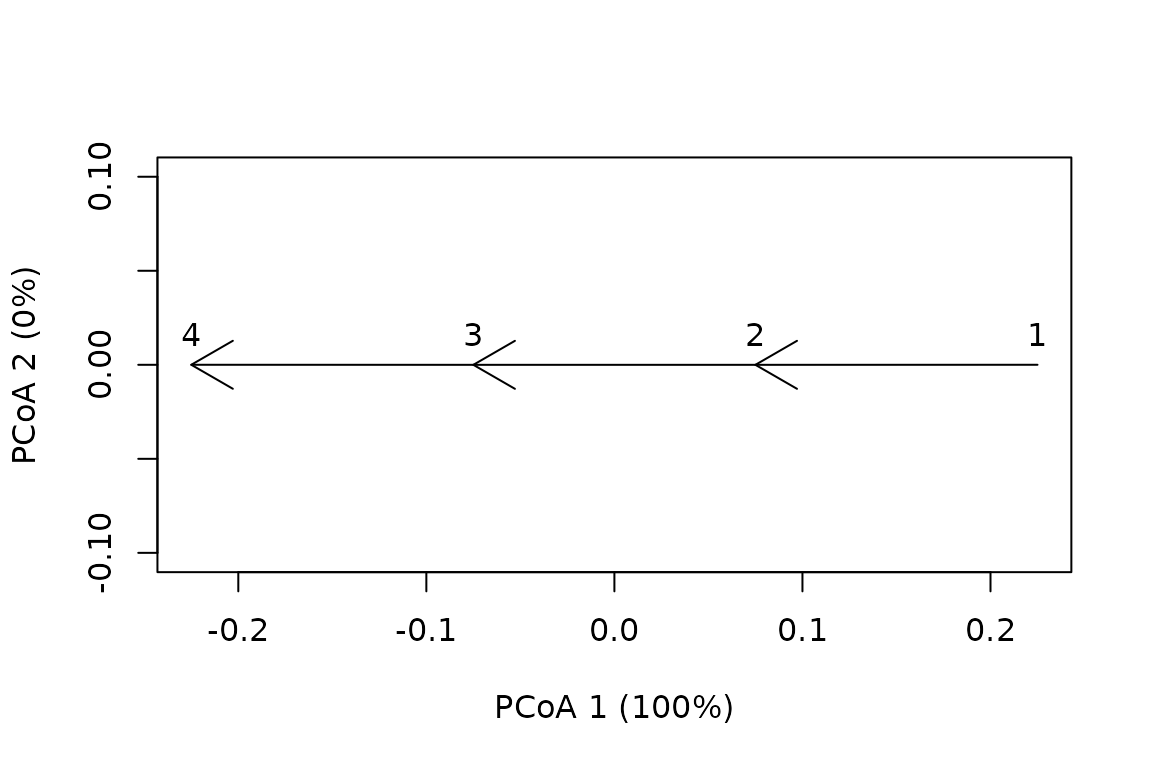

Here we see that Bray-Curtis dissimilarity responds linearly to the proposed sequence of community dynamics. To confirm this geometry, we can calculate the geometric properties of the trajectory (i.e. length, angle between consecutive segments and overall directionality):

trajectoryLengths(D,sites,surveys)

##     S1   S2   S3 Trajectory
## 1 0.15 0.15 0.15       0.45

trajectoryAngles(D,sites,surveys)

##   S1-S2 S2-S3 mean sd rho
## 1     0     0    0  0   1

trajectoryDirectionality(D,sites,surveys)

## 1 
## 1

Angles are 0 degrees and overall directionality is maximum (i.e. 1), in accordance with the plot and the data. We now proceed to take the square root of the dissimilarity values, as would be necessary to achieve a metric (and Euclidean) space in a more complex data set:

sqrtD = sqrt(D)
sqrtD

##           1         2         3
## 2 0.3872983                    
## 3 0.5477226 0.3872983          
## 4 0.6708204 0.5477226 0.3872983

The transformation increases all dissimilarity values (because the original values are smaller than 1), but the increase is larger for smaller values, so the ratio between large dissimilarities and small dissimilarities decreases. This has an effect on the overall shape of the trajectory, which surprisingly now looks like:

trajectoryPCoA(sqrtD,sites,surveys, survey.labels = T)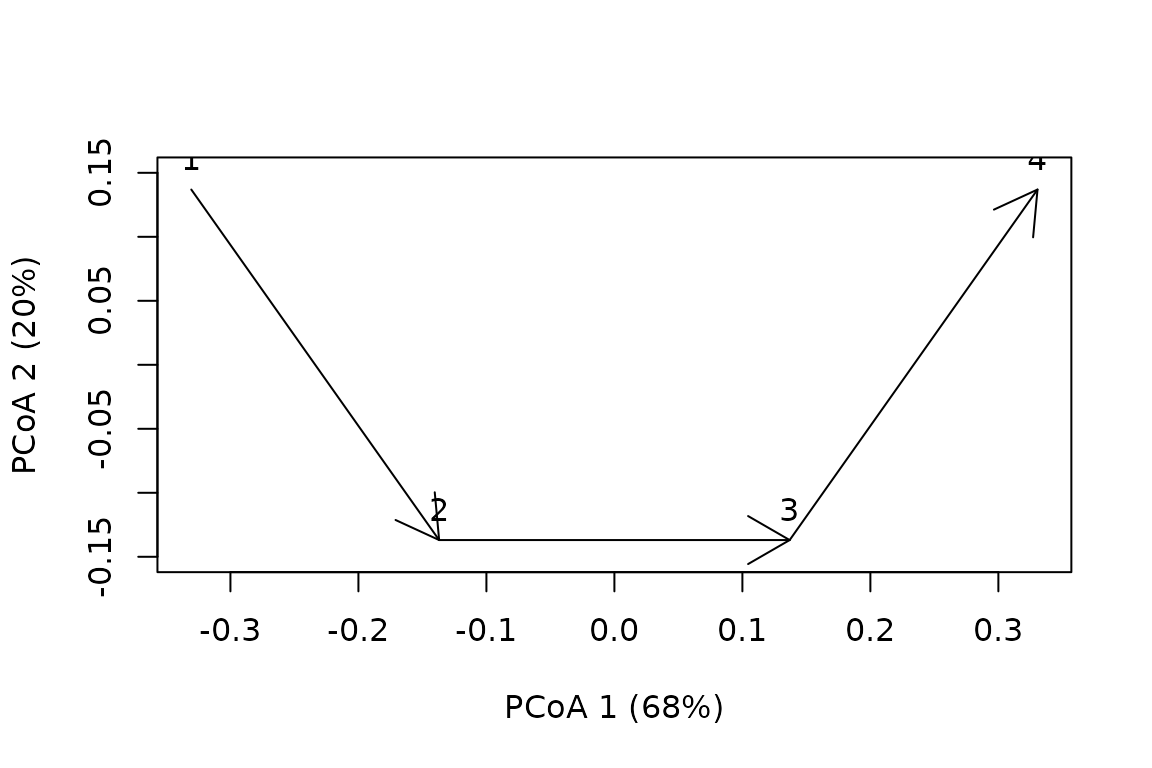

In addition to the distortion observed, the number of dimensions of the data have increased (i.e the sum of variance explained by the two axes is 88% < 100%), so we cannot be sure that the angles are well represented. If we re-calculate the properties of the trajectory taking into account all dimensions we obtain:

trajectoryLengths(sqrtD,sites,surveys)

##          S1        S2        S3 Trajectory
## 1 0.3872983 0.3872983 0.3872983   1.161895

trajectoryAngles(sqrtD,sites,surveys)

##   S1-S2 S2-S3 mean sd rho
## 1    90    90   90  0   1

trajectoryAngles(sqrtD,sites,surveys, all=TRUE)

##   A1 A2 A3 A4 mean sd rho
## 1 90 90 90 90   90  0   1

trajectoryDirectionality(sqrtD,sites,surveys)

##   1 
## 0.5

The length of segments and the trajectory have increased, but all segments are of the same length, in agreement with the original trajectory. In contrast, the angles are now 90 degrees and the overall directionality has decreased substantially.

3. Effect of different transformations on more complex trajectories

Here we use simulated data to compare four transformation approaches:

Local transformation of semi-metric dissimilarities (such as the percentage difference) in every triplet when the triangle inequality is required. This is done by default in the CTA functions of package vegclust.
Global transformation of dissimilarities, using the square root.
Global transformation of dissimilarities by using Principal Coordinates Analysis (classical multidimensional scaling) with eigenvalue correction.
Global transformation of dissimilarities by using metric multidimensional scaling (metric MDS).

We use simulated dynamics to build another trajectory with more species (20) and more time steps. We begin by setting the number of time steps (50) and the size of the community (50 individuals):

Nsteps = 50
CC = 50
Nreplace <- CC*0.05

Nreplace is the number of individuals to be replaced each time step (5%). Now we define the initial community vector and the vector with the probabilities of offspring for each species according to some ecological conditions:

x <- c(0, 1, 0, 67, 1, 3, 0, 2, 2, 2, 1, 6, 2, 0, 0, 2, 5, 1, 6, 0)
poffspring <- c(0, 0, 0.002, 0.661 ,0 ,0, 0.037, 0.281, 0, 0, 0, 0.008, 0, 0, 0.005, 0.003, 0, 0, 0, 0)

We can now simulate the dynamics by sequentially applying stochastic deaths and recruitment:

m <- matrix(0, nrow=Nsteps+1, ncol=length(x))
m[1, ] = x
for(k in 1:Nsteps) {
  pdeath <-x/sum(x) #Equal probability of dying
  deaths<-rmultinom(1,Nreplace, pdeath)
  x <- pmax(x - deaths,0)
  offspring = rmultinom(1,Nreplace, as.vector(poffspring))
  x <- x + offspring
  m[k+1, ]<-x
}

Then we decide how frequently (with respect to the simulated step) a sample of the community is taken, here every four steps:

Sj <- seq(1,Nsteps+1, by=4) #Sample every four steps
mj <- m[Sj,]
surveys = 1:length(Sj)
sites = rep(1,length(Sj))

Now we are ready to calculate the Bray-Curtis dissimilarity:

D <- vegan::vegdist(mj,"bray")

In this more complex trajectory, some triangles may not obey the triangle inequality (depending on the simulation). This can be inspected using function is.metric:

is.metric(D, tol=0.0000001)

## [1] TRUE

Deviations from a metric space, if they exist, will be small, so that local transformation of triangles will be very small.

Local transformations are not possible to display trajectories. When we plot the trajectory using function trajectoryPCoA the global transformation of principal coordinates analysis (PCoA) with negative eigenvalue correction is performed. This is fine to display trajectories, but has problems when measuring angular properties, as we will see.

pcoa<-trajectoryPCoA(D, sites, surveys, selection=1,length=0.1, axes=c(1,2), survey.labels = T)

## Warning in cmdscale(D2, eig = TRUE, add = TRUE, k = nrow(as.matrix(D2)) - :
## only 11 of the first 12 eigenvalues are > 0

## Warning in arrows(x[niini], y[niini], x[nifin], y[nifin], ...): zero-length
## arrow is of indeterminate angle and so skipped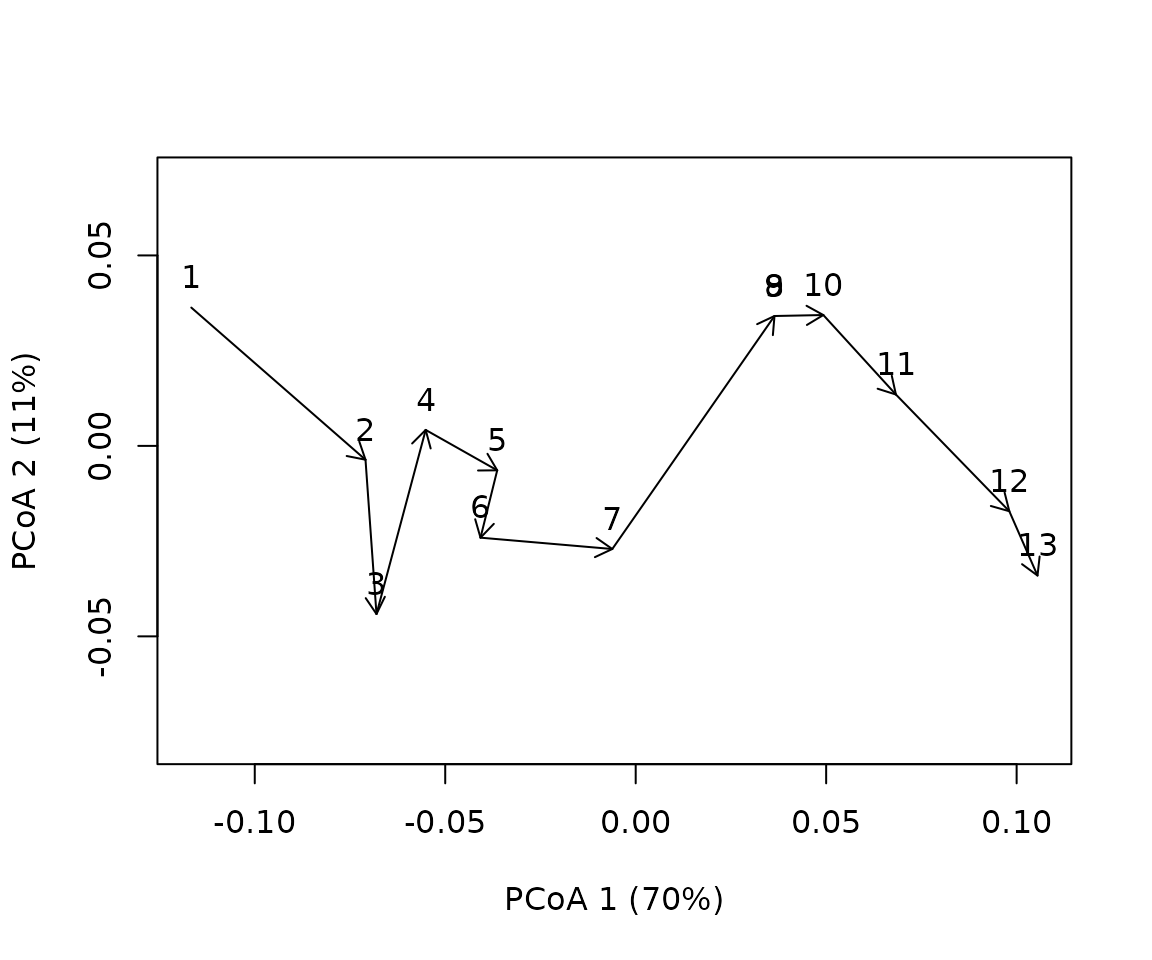

pcoaD = dist(pcoa$points)

The trajectory has some twists derived from stochasticity in death and recruitment. Let’s now look at the square root of the Bray-Curtis dissimilarity:

sqrtD = sqrt(D)
pcoaSqrt = trajectoryPCoA(sqrtD, sites, surveys, selection=1,length=0.1, axes=c(1,2), survey.labels = T)

## Warning in arrows(x[niini], y[niini], x[nifin], y[nifin], ...): zero-length
## arrow is of indeterminate angle and so skipped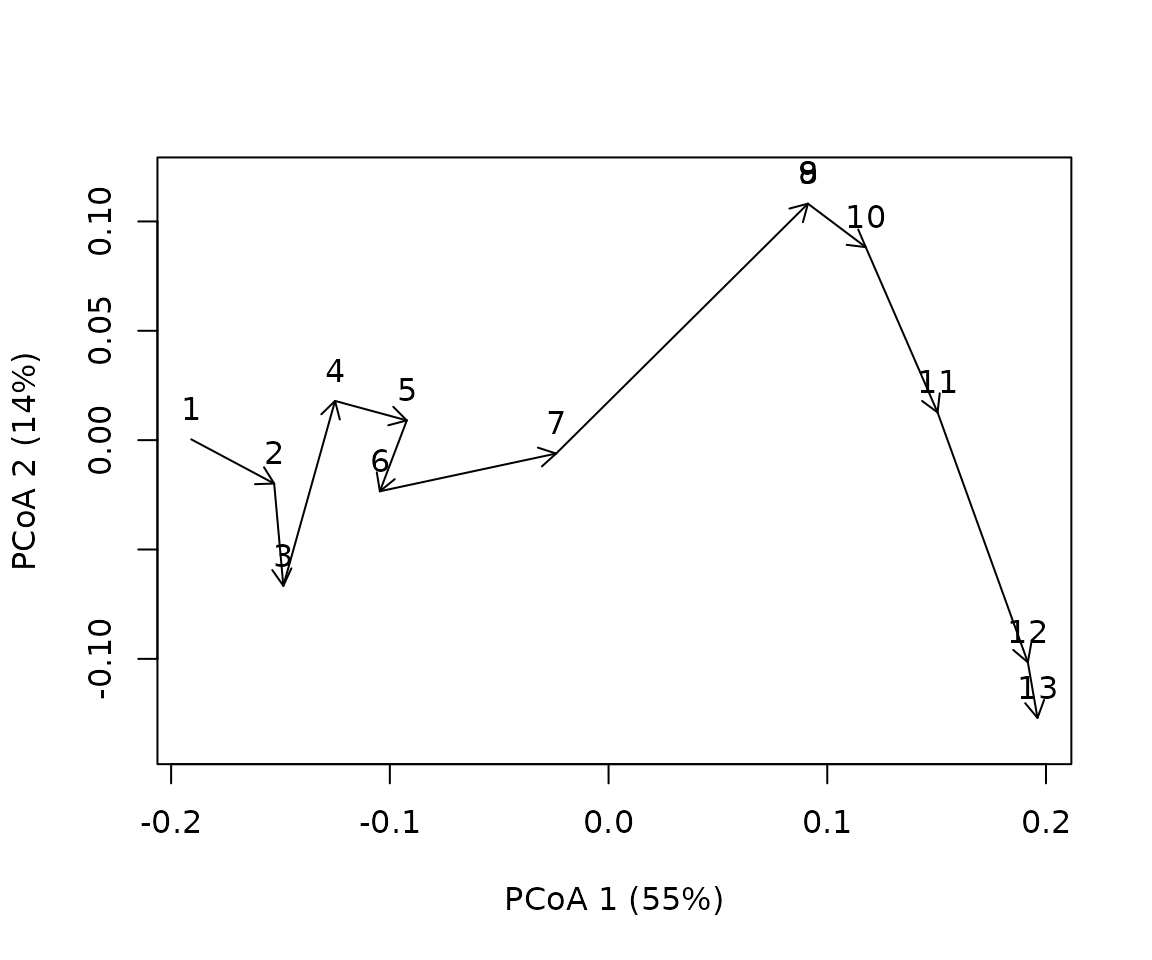

Finally, we also transform dissimilarities using metric multidimensional scaling (mMDS), provided by package smacof:

res <- smacof::mds(D, ndim = length(Sj)-1, type = "interval")
mmdsD <- dist(res$conf)
trajectoryPlot(res$conf, sites, surveys, selection=1,length=0.1, axes=c(1,2), survey.labels = T)

## Warning in arrows(xp[niini], yp[niini], xp[nifin], yp[nifin], ...): zero-length
## arrow is of indeterminate angle and so skipped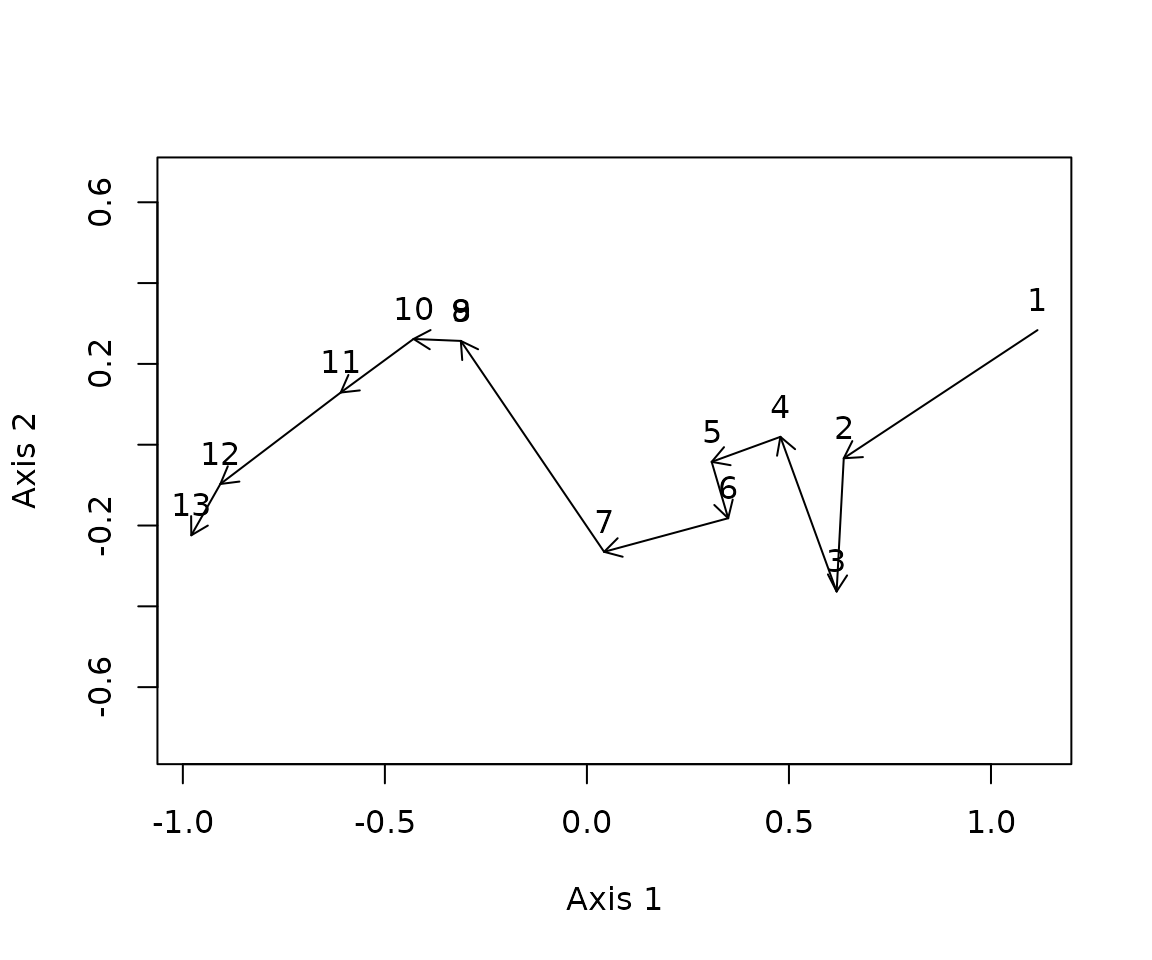

While the three plots look different, the differences are not striking (besides rotation issues). We can compare the stress of the global solutions:

smacof::stress0(D,pcoaSqrt$points, type="interval")

## 
## Call:
## smacof::stress0(delta = D, init = pcoaSqrt$points, type = "interval")
## 
## Model: Symmetric SMACOF 
## Number of objects: 13 
## Stress-1 value: 0.077 
## Number of iterations: 0

smacof::stress0(D,pcoa$points, type="interval")

## 
## Call:
## smacof::stress0(delta = D, init = pcoa$points, type = "interval")
## 
## Model: Symmetric SMACOF 
## Number of objects: 13 
## Stress-1 value: 0.007 
## Number of iterations: 0

smacof::stress0(D,res$conf, type="interval")

## 
## Call:
## smacof::stress0(delta = D, init = res$conf, type = "interval")
## 
## Model: Symmetric SMACOF 
## Number of objects: 13 
## Stress-1 value: 0.013 
## Number of iterations: 0

Where we see that the square root leads to the strongest alteration of original dissimilarities. If we calculate geometric properties we are not limited by ordination plots and we can take into account all dimensions.

anglesD = trajectoryAngles(D,sites,surveys)
anglesSqrtD = trajectoryAngles(sqrtD,sites,surveys)
anglesPcoaD = trajectoryAngles(pcoaD,sites,surveys)
anglesmmdsD = trajectoryAngles(mmdsD,sites,surveys)

df<-as.data.frame(rbind(anglesD, anglesSqrtD, anglesPcoaD, anglesmmdsD))
row.names(df)<-c("local", "global.sqrt", "global.pcoa", "global.mmds")
round(df,2)

##             S1-S2  S2-S3  S3-S4 S4-S5  S5-S6  S6-S7 S7-S8 S8-S9 S9-S10 S10-S11
## local        0.00  75.52  82.82  0.00  97.18 104.48  0.00  0.00    NaN     NaN
## global.sqrt 90.00 101.78 104.48 90.00 104.48 110.70 90.00 90.00    NaN     NaN
## global.pcoa 80.72  98.29 103.57 77.78 104.99 112.42 91.92 91.92 105.24  102.26
## global.mmds 54.83  95.78  95.60 44.20  97.89 119.23 72.23 49.85  93.77   92.68
##             S11-S12  mean   sd  rho
## local          0.00 38.10 0.83 0.71
## global.sqrt   90.00 96.81 0.14 0.99
## global.pcoa   80.72 95.46 0.19 0.98
## global.mmds   21.88 76.70 0.50 0.88

The first call to trajectoryAngles with matrix D represents the default strategy of transforming triangles locally, which involves the weakest transformation of all and can be taken as reference. Both the square root and PCoA with negative eigenvalue correction induce a strong transformation of trajectory angles. The global solution of metric MDS leads to angles that are more similar to those of the local transformation strategy.

If we inspect the overall directionality, the global solution of metric MDS provides a value that is again closer to that of local transformation, compared to PCoA and the square root:

trajectoryDirectionality(D,sites,surveys)

##         1 
## 0.8770056

trajectoryDirectionality(sqrtD,sites,surveys)

##         1 
## 0.4810576

trajectoryDirectionality(pcoaD,sites,surveys)

##         1 
## 0.5927582

trajectoryDirectionality(mmdsD,sites,surveys)

##         1 
## 0.7532264

4. Conclusions

In this small study we compared the effect of different solutions to violation of the triangle inequality. If function is.metric returns TRUE for a given data set one should not worry about violations of the triangle inequality. Local solutions are those that imply the smallest number of changes, but these will not be consistent across triplets, so users may desire to apply a global transformation that produces euclidean spaces. This should be done with care. We have shown how the square root transformation distorts the angles and overall directionality of trajectories on the space defined by the percentage difference (alias Bray-Curtis) dissimilarity index. We suspect that this negative effect of square root transformation on angles happens no matter which coefficient is used to derive the initial distance matrix. Therefore, we advocate for avoiding its use when conducting community trajectory analysis (in particular for angles). The global transformation consisting in the application of PCoA with negative eigenvalue correction is less strong than the square root, but it still strongly change the angles between segments. Perhaps, the less harmful global transformation is provided by metric Multidimensional Scaling, but the need to embed distances in an Euclidean space of all three transformations implies a stronger requirement than being a metric, and results in distortions.

Miquel De Cáceres

2024-08-26

1. Introduction

2. Effect of square root on a simple directional trajectory

3. Effect of different transformations on more complex trajectories

4. Conclusions