Meta-modelling exercise

Introduction

Goal

This document presents a meta-modelling exercise between basic (under Granier’s transpiration) and advanced (under Sperry’s transpiration mode) versions of the soil plant water balance model. The goal is to make transpiration and photosynthesis predictions produced by the basic water balance model as similar as possible to those produced by the advanced model which, given its greater process detail and physical basis, is assumed to provide more realistic and accurate predictions when appropriate functional traits are supplied. Such exercise was included, among others, in De Cáceres et al. (2023).

The meta-modelling results should benefit not only water balance simulations (function spwb) but also simulations of forest growth (growth) and dynamics (fordyn). The results presented here were obtained using ver. 4.7.0 of medfate.

Target parameters

The following parameters are used in the basic model, that cannot easily be parameterized from available information (see https://emf-creaf.github.io/medfatebook/index.html):

Tmax_LAI and Tmax_LAIsp, which determine the ratio of maximum transpiration over potential evapotranspiration for a given LAI. An empirical function with these parameters was derived by Granier (1999) for European temperate forests, without distinguishing between forests dominated by different species.
Psi_Extract and Exp_Extract, which determine the actual transpiration as a fraction of maximum transpiration, as a function of soil water potential for a given layer.
WUE, which represents the daily water use efficiency (g C of gross assimilation / l H2O transpired) under conditions of VPD = 1kPa, high photosynthetically active radiation (PAR) and no air CO2 limitations.
WUE_par, which specifies the dependency of WUE on PAR.
WUE_co2, which specifies the dependency of WUE on air CO2 concentration.
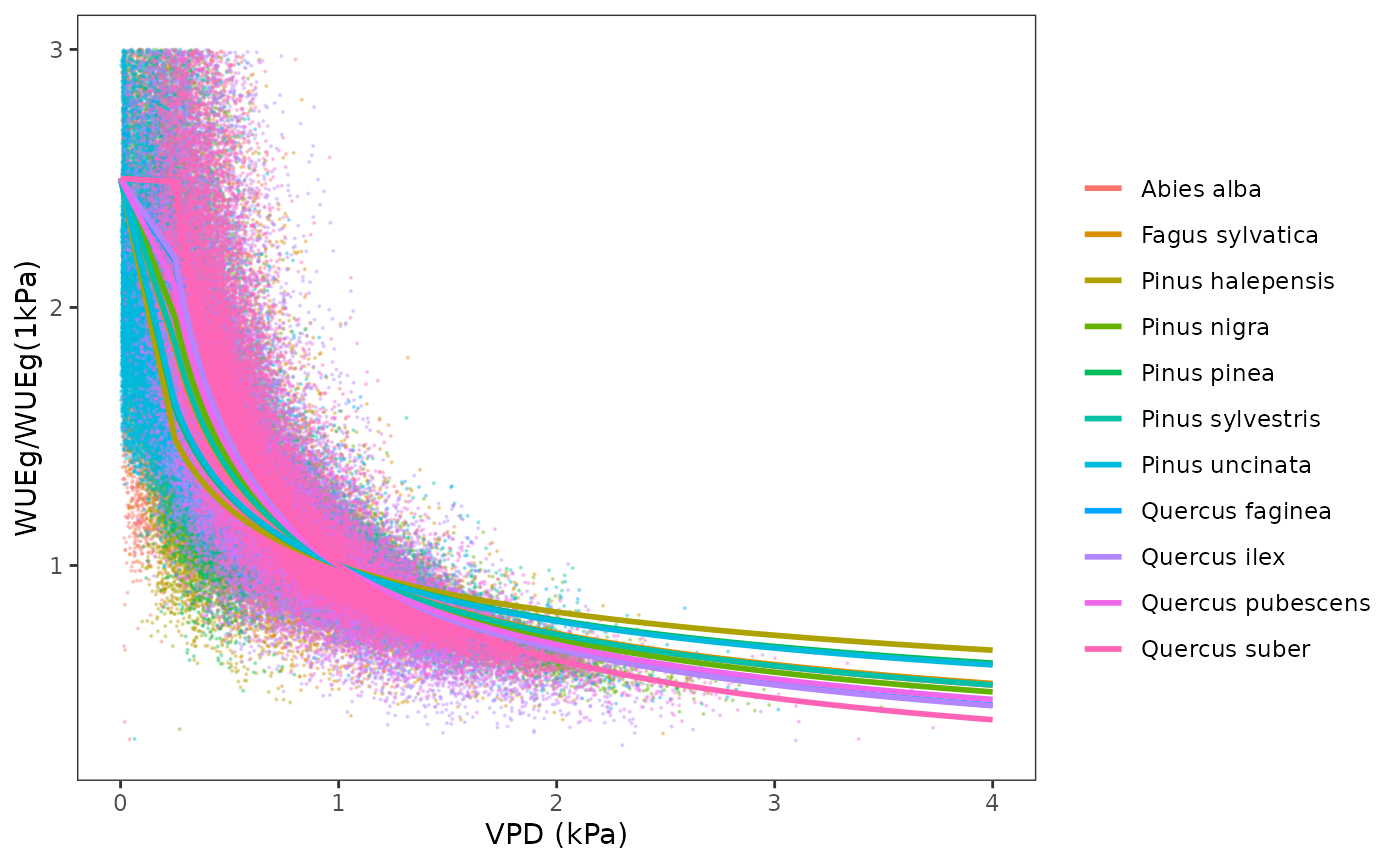
WUE_vpd, which specifies the dependency of WUE on vapor pressure deficit (VPD).

As stated above, the general idea is to use simulation results issued by the advanced water balance model to obtain appropriate species-level estimates of the previous parameters, so that simulations with the basic water balance model (which is faster) produce an output similar that of the advanced model (which is slower). In the case of Tmax_LAI and Tmax_LAIsp we aim to determine a species-specific factor that can be used to modify the empirical coefficients obtained by Granier (1999). Water use efficiency is an emergent property of the advanced water balance model, depending on multiple parameters (hydraulics, photosynthetic capacity, stomatal conductance, etc). We can thus estimate WUE values (for [CO2] = 386) using simulations with high light levels and no water deficit. The decrease of WUE for plant cohorts in progressively shadier environments with respect to WUE under full light can provide us with an estimate of WUE_par, which again will depend on multiple plant traits. Finally, we can use additional simulations of the complex model under increasing [CO2] values to model the relationship between gross photosynthesis at a given [CO2] compared to [CO2] = 386 for each species.

Target species

The metamodelling procedure could be applied to any target species, but we focused on twelve main tree species in Catalonia: Abies alba, Castanea sativa, Pinus halepensis, Pinus sylvestris, Pinus nigra, Pinus uncinata, Pinus pinea, Quercus faginea, Quercus ilex, Quercus pubescens, Quercus suber and Fagus sylvatica. These species are included in the species parameter table SpParamsMED from package medfate.

For each of those species, we first revised the values of the most important parameters in the advanced water balance model (parameters of the hydraulic vulnerability curve are omitted as they should not be relevant in simulations without soil water deficit):

Name	SLA	Al2As	VCleaf_kmax	Kmax_stemxylem	Gswmax	Vmax298	Jmax298
Abies alba	7.768174	7194.245	6	1.3000000	0.2300000	58.08712	103.28235
Castanea sativa	13.862317	5000.000	8	1.0000000	0.3500000	51.34505	93.03424
Fagus sylvatica	18.320000	2076.120	8	0.9000000	0.3350000	94.50000	159.90000
Pinus halepensis	5.140523	1317.523	4	0.1500000	0.2850000	72.19617	124.16865
Pinus nigra	4.569508	1272.265	5	0.4100000	0.2366667	68.50296	118.76713
Pinus pinea	4.207291	1615.509	4	0.2500000	0.2366667	72.42173	124.49715
Pinus sylvestris	4.897943	1598.180	5	0.4500000	0.2366667	83.00000	143.00000
Pinus uncinata	3.804390	1608.774	5	0.6895376	0.2366667	73.41275	125.93862
Quercus pubescens	11.800000	6031.582	6	0.7000000	0.2787500	57.33919	102.15484
Quercus ilex	6.340000	3908.823	4	0.4000000	0.2007222	68.51600	118.78628
Quercus faginea	8.328895	4189.325	6	0.7000000	0.2787500	71.21535	122.73836
Quercus suber	8.656130	4189.325	4	0.4000000	0.2862500	70.27833	121.36913

Ideally, the transpiration and photosynthesis predictions of the advanced water balance model should be evaluated with these parameterization before using it as reference for the meta-modelling study. Otherwise we could be biasing both models with inappropriate parameter values. At present, the advance water balance model has been evaluated using data from experimental plots in stands dominated by some of the target species, but not others.

Simulations for the meta-modelling exercise

Forest, soil and weather inputs

We used forest plot data from the third edition of the Spanish National Forest Inventory (IFN3). Forest plots were located in Catalonia and with a minimum basal area of 5 $m^2·ha^{-1}$ . For each target species we randomly selected up to 50 forest plots where the species was dominant (> 50% in basal area). Plant records corresponding to species different than the target species were excluded.

Like in other simulation exercises with IFN data, soil data was obtained from SoilGrids from plot coordinates, with rock fragment contents corrected according to the amount of surface stoniness recorded in the field sampling. Daily weather data corresponding to year 2000 was obtained by interpolation using package meteoland on the location of each forest plot.

Soil water balance simulations

For each target species, we ran the soil water balance model using function spwb (actually, spwb_spatial() from package medfateland) and either Granier’s or Sperry’s transpiration mode. Simulations were conducted using control$unlimitedSoilWater = TRUE so that transpiration and photosynthesis estimates did not include soil water limitations (cohorts in the shade were still affected by the lower PAR, however). For each plant cohort in each simulated plot we recorded the percentage of PAR available to the plant cohort, the annual transpiration and annual photosynthesis produced by each model.

Additional simulations with increasing carbon dioxide concentration were conducted using the Sperry transpiration mode and $[CO_2]$ values increasing from 350 ppm to 900 ppm. We also avoided soil water limitations using control$unlimitedSoilWater = TRUE. For each plot we recorded the annual gross photosynthesis per leaf area averaged across plant cohorts using their LAI as weights.

Transpiration ratio

We examined if there were systematic differences in annual transpiration (E) between the two models. Such differences should be species-specific. While the basic model has a single linear equation (from Granier) to estimate the ratio maximum transpiration (Tmax) to potential evapotranspiration (PET) from stand’s LAI and then divides plant transpiration among plant cohorts, the advanced model estimates cohort transpiration from a complex calculation involving several species-specific functional traits. The ratio between cohort annual E estimates from the two models could be used to scale the estimates of Granier’s equation (or in other words, to scale its parameters).

The following plot displays the ratio between cohort annual E estimates obtained using the basic and advanced models, where we use the percentage of PAR of the plant cohort in the x-axis to show whether the relationship changes between sunlit or shade cohorts:

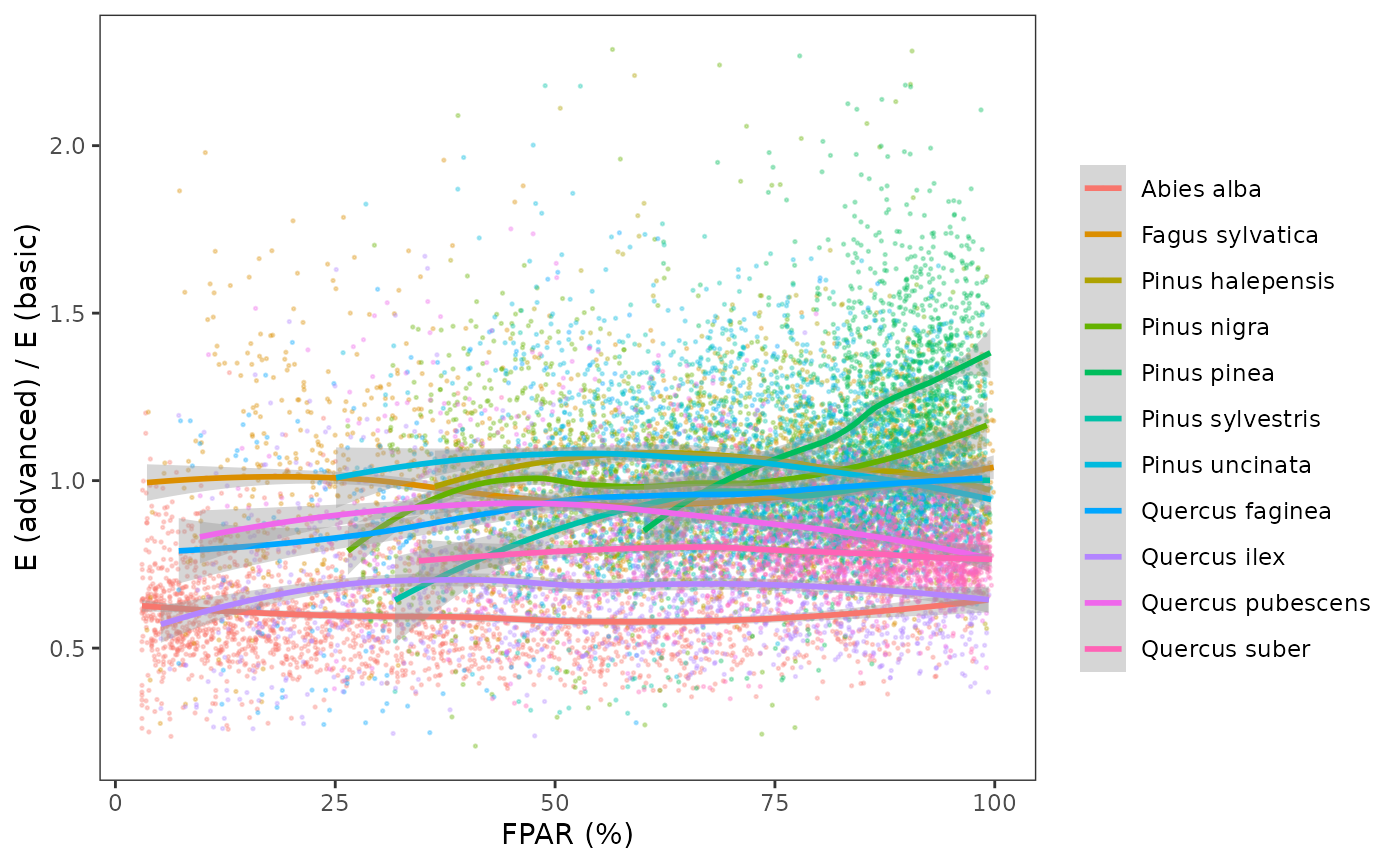
It is evident that there are differences in the average ratio across species and apparently this ratio does not change with the vertical position of the cohort within the canopy. We can estimate species-average ratios and use them to multiply the default coefficients of Granier’s (1999) equation (default values for parameters Tmax_LAI = 0.134 and Tmax_LAIsq = -0.006).

Name	n	E_ratio_mean	E_ratio_sd	E_ratio_se	Tmax_LAI	Tmax_LAIsq
Abies alba	1387	0.6621066	0.1569041	0.0042130	0.0887223	-0.0039726
Castanea sativa	1034	0.8540850	0.1757506	0.0054656	0.1144474	-0.0051245
Fagus sylvatica	1225	1.1567050	0.2250004	0.0064286	0.1549985	-0.0069402
Pinus halepensis	783	1.3954096	0.2296720	0.0082078	0.1869849	-0.0083725
Pinus nigra	992	1.1691691	0.1961093	0.0062265	0.1566687	-0.0070150
Pinus pinea	837	1.7054336	0.2460283	0.0085040	0.2285281	-0.0102326
Pinus sylvestris	1109	1.1743648	0.1918681	0.0057615	0.1573649	-0.0070462
Pinus uncinata	1510	1.1089369	0.2057106	0.0052938	0.1485975	-0.0066536
Quercus faginea	669	1.3353312	0.2515112	0.0097240	0.1789344	-0.0080120
Quercus ilex	840	0.9336025	0.2308113	0.0079637	0.1251027	-0.0056016
Quercus pubescens	797	1.1658803	0.2277965	0.0080690	0.1562280	-0.0069953
Quercus suber	1058	1.1666327	0.1440836	0.0044297	0.1563288	-0.0069998

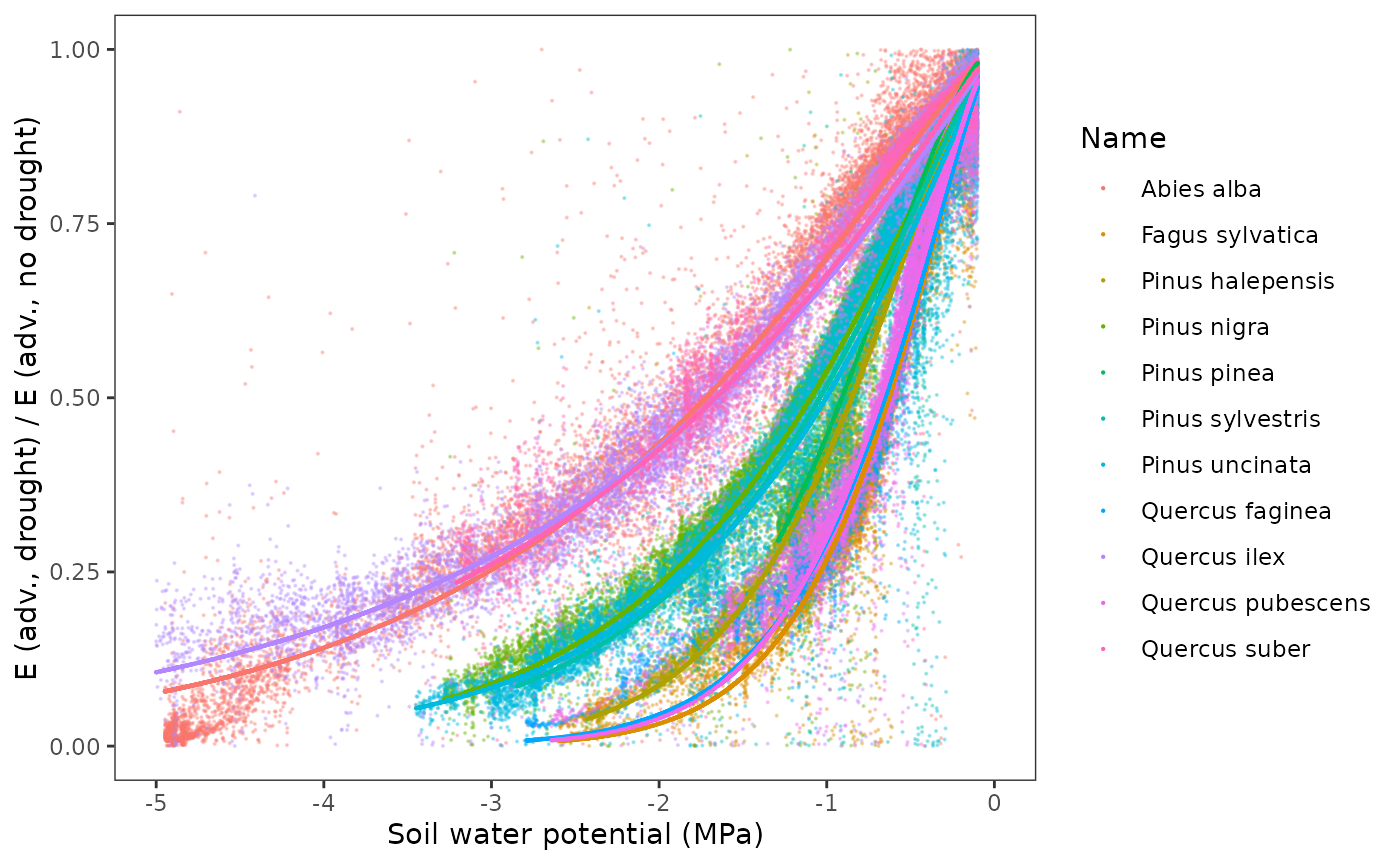
Relative transpiration function

Parameters Psi_Extract and Exp_Extract determine the actual transpiration as a fraction of maximum transpiration, as a function of soil water potential for a given layer. They are parameters of a Weibull function. They can be estimated by fitting the Weibull function to the ratio of transpiration values obtained in simulations with vs without soil drought limitations (under Sperry’s transpiration mode) as a function of soil water potential. This is illustrated in the figure below for the different species:

Water use efficiency ([CO2] = 386)

Relationship between WUE and PAR

We estimated WUEg as the ratio between annual gross photosynthesis (Ag) and annual transpiration (E), both estimated using the advanced transpiration model. WUE values thus depend on the species identity (via functional traits) and on plot environmental factors (e.g. climatic conditions), as well as on the position of the plant within the canopy. We then estimate the maximum PAR and maximum WUE across cohorts for each plot, and calculate the relative WUE for each cohort as the ratio between WUE and the plot maximum value.

We want to build a model of the relative WUE as a function of available PAR, so that we can reduce species-level maximum WUE values for cohorts in the shadow. To fit such model we need good estimates of relative WUE, because this implies that the maximum WUE values correspond to high PAR. With this aim, we focus on those records corresponding to plots/species where at least 90% of PAR was available for at least one cohort of the species in the plot.

Using this selection, we then draw the relationship between PAR and WUEg:

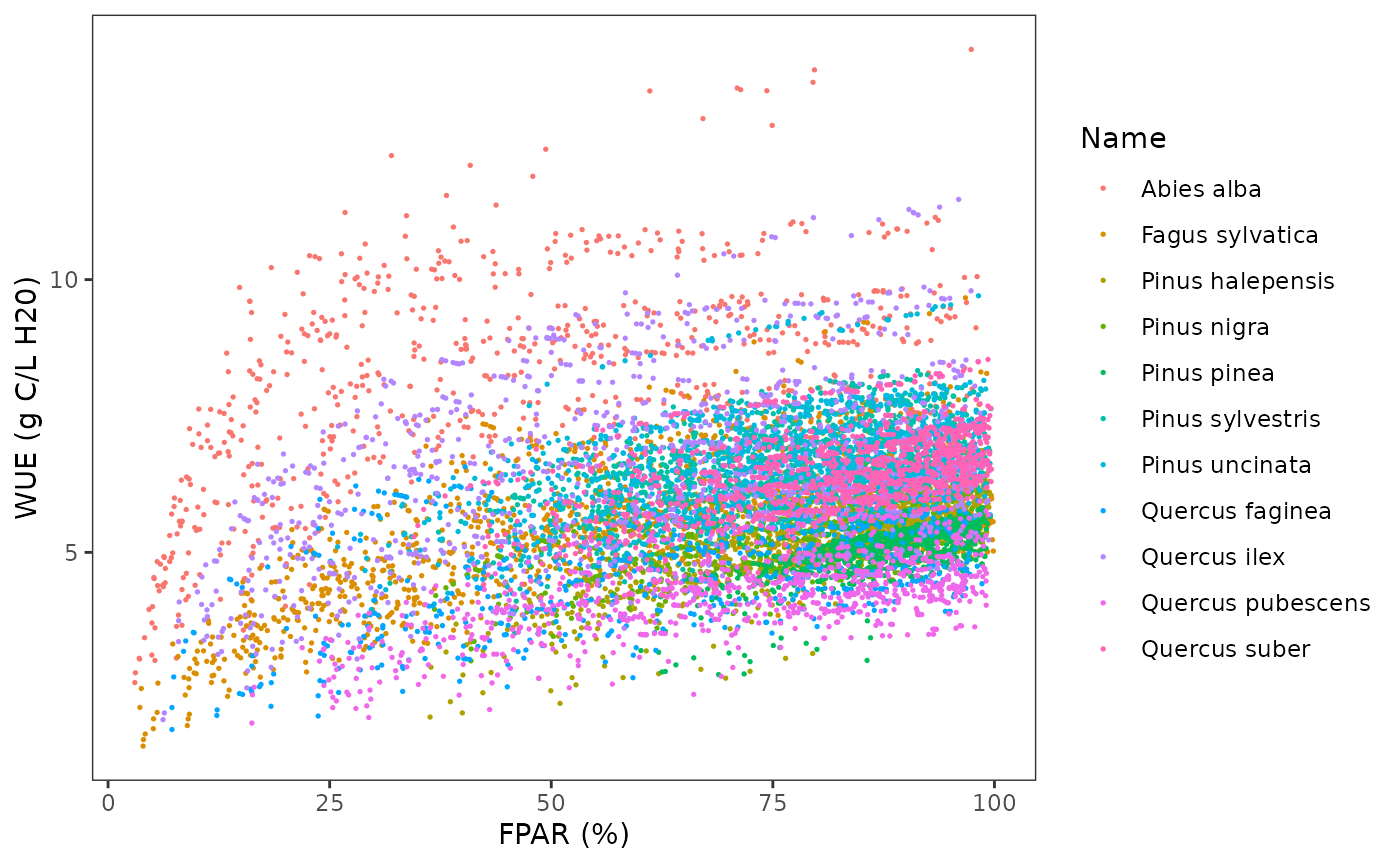
where we see that the relationship is species-specific. WUE is known to decrease for parts of the canopy receiving less light (e.g. Medrano et al. 2012). We can now plot relative WUE in relationship to FPAR:

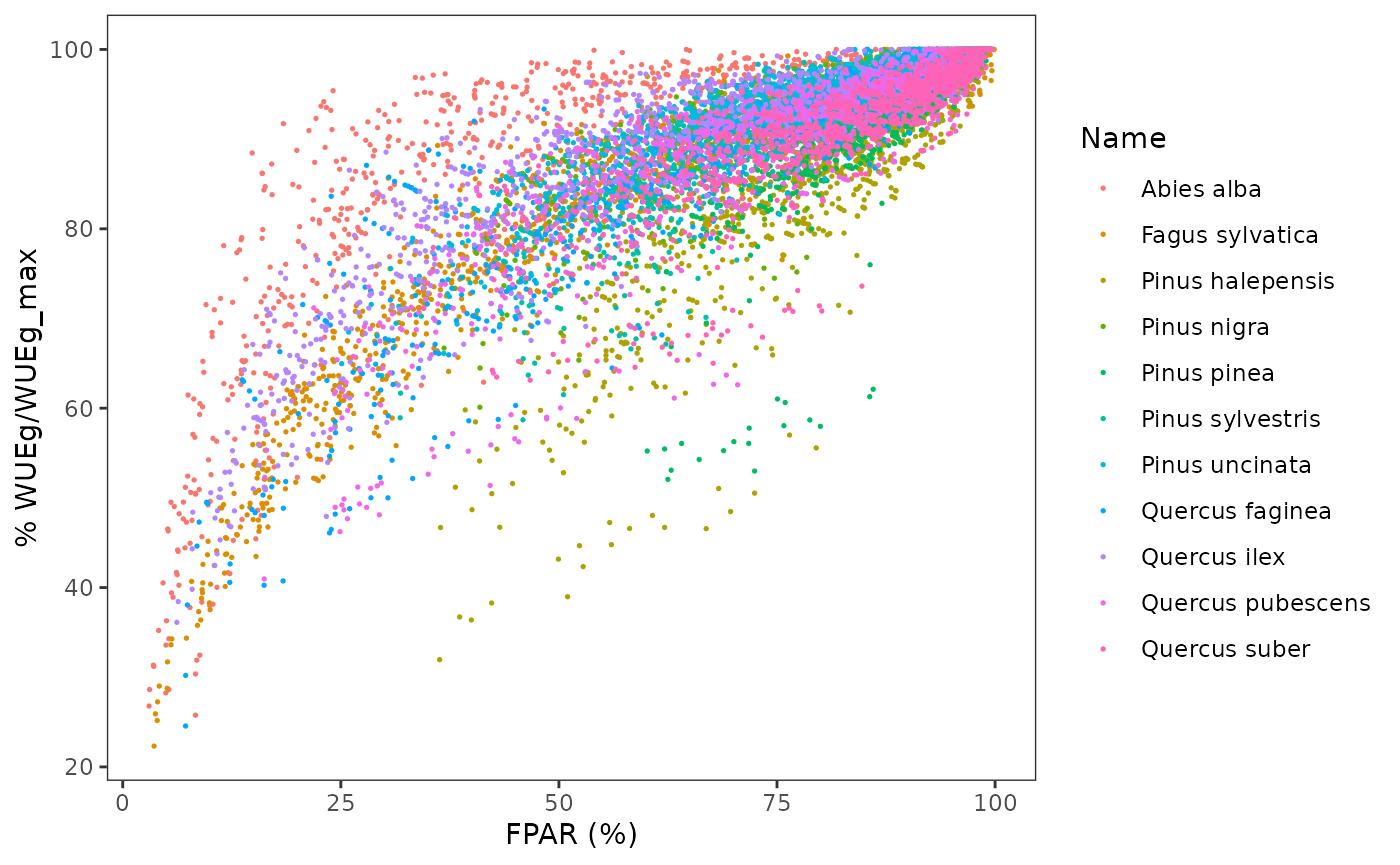
Note that the relationship between relative WUE and PAR is less noisy than the relationship between absolute WUE and FPAR. For each species, we fit a non-linear model where relative WUE is a power function of FPAR:

We now draw again the previous plot with the species-specific fitted relationships, i.e. relative WUEg as a function of FPAR:

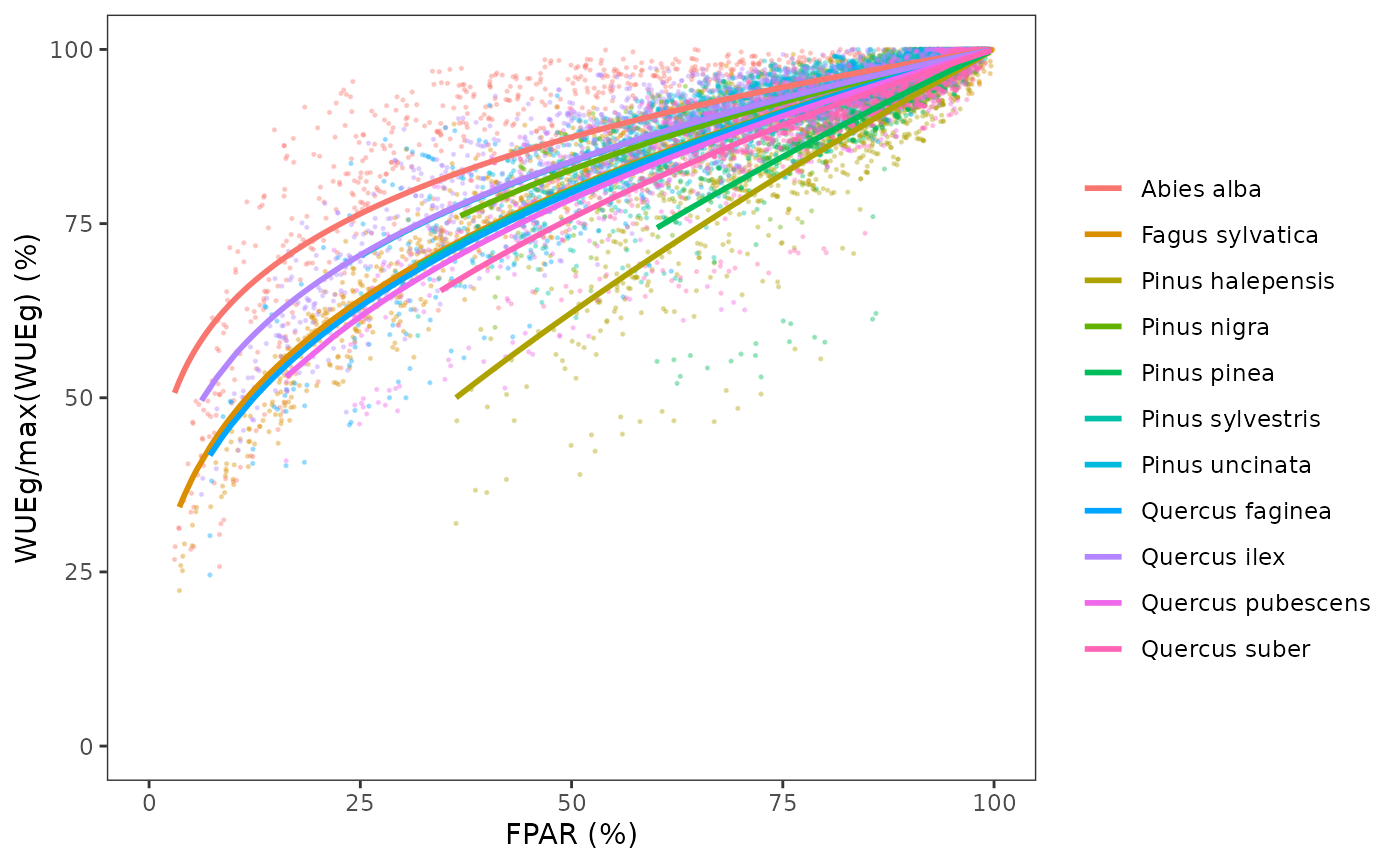
Note that there are substantial differences in the decay coefficients among species.

Relationship between WUE and VPD

Dependency of photosynthesis on [CO2]

The parameter WUE_co2, which specifies the dependency of WUE on air CO2 concentration is estimated by fitting a non-linear function on the ratio of photosynthesis under a given $[CO_2]$ value over the photosynthesis at $[CO_2] = 386$ ppm:

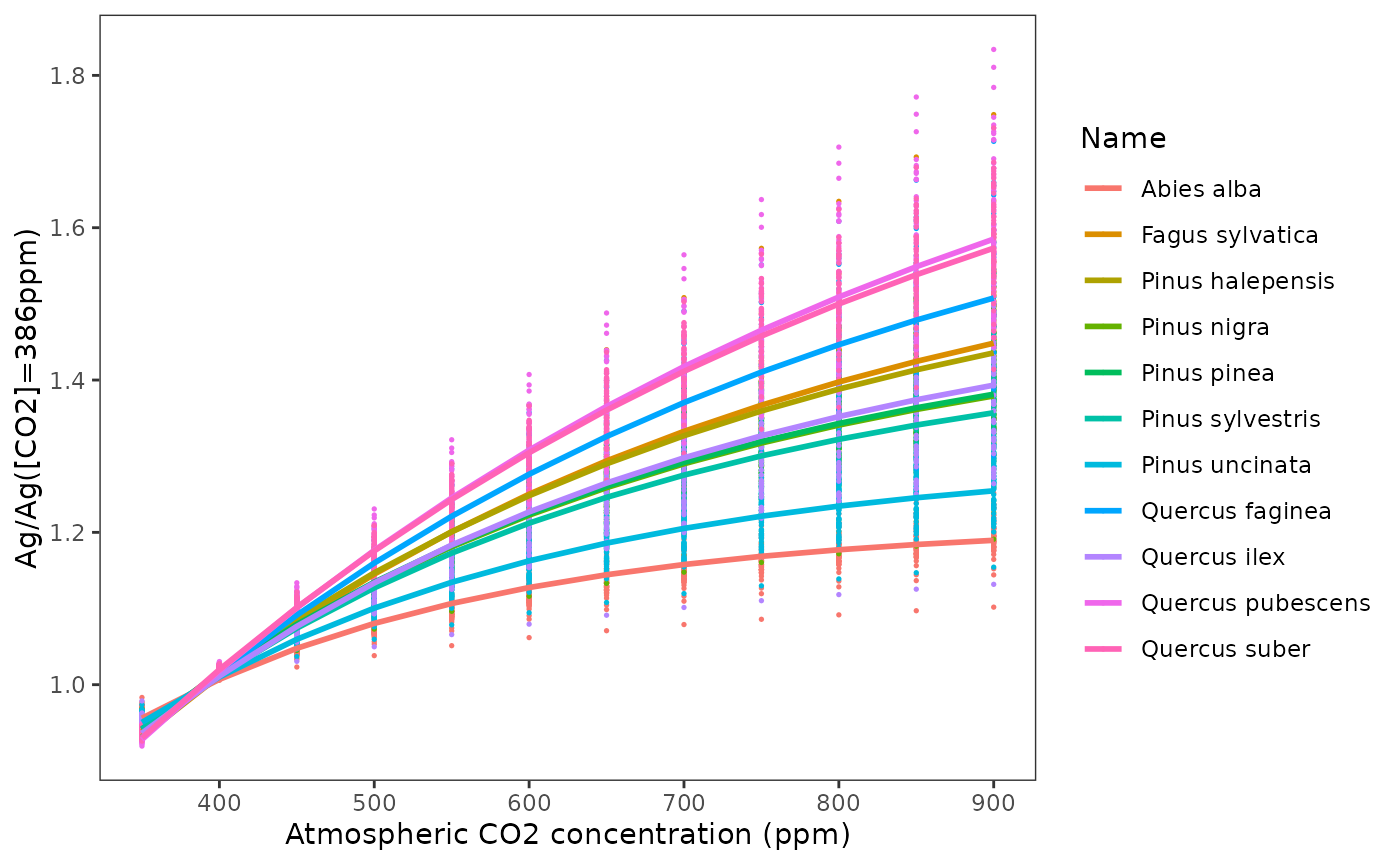
Meta-modelling parameters

The table containing the five parameters estimated via meta-modelling is the following:

Name	Tmax_LAI	Tmax_LAIsq	Psi_Extract	Exp_Extract	WUE	WUE_par	WUE_co2	WUE_vpd
Abies alba	0.0887223	-0.0039726	-1.7470147	1.479139	8.536401	0.1540396	0.0043216	-0.3781743
Castanea sativa	0.1144474	-0.0051245	-0.7786090	1.398753	8.215770	0.1070242	0.0024625	-0.4673612
Fagus sylvatica	0.1549985	-0.0069402	-0.7291183	1.404854	9.420308	0.1542946	0.0021851	-0.4061310
Pinus halepensis	0.1869849	-0.0083725	-0.9218219	1.504542	8.525550	0.5239136	0.0025863	-0.2647169
Pinus nigra	0.1566687	-0.0070150	-1.2504241	1.299411	7.924382	0.1553481	0.0028494	-0.4368847
Pinus sylvestris	0.1573649	-0.0070462	-1.1850580	1.325987	8.678368	0.1708214	0.0030029	-0.4128647
Pinus pinea	0.2285281	-0.0102326	-0.9649847	1.491201	7.156091	0.5190786	0.0028180	-0.3578795
Pinus uncinata	0.1485975	-0.0066536	-1.1278875	1.247934	6.725716	0.1355138	0.0039610	-0.2947655
Quercus faginea	0.1789344	-0.0080120	-0.7696372	1.390459	8.570752	0.1549808	0.0018383	-0.5006765
Quercus ilex	0.1251027	-0.0056016	-1.9726871	1.149052	8.968208	0.1412266	0.0024131	-0.5664879
Quercus pubescens	0.1562280	-0.0069953	-0.8145007	1.422054	8.787211	0.1491588	0.0018327	-0.5140889
Quercus suber	0.1563288	-0.0069998	-1.7650814	1.607616	9.659193	0.1498707	0.0019227	-0.6104881

Evaluation of the effect of the new parameters

Here we evaluated whether the estimated parameters indeed increased the similarity of transpiration (E) and gross photosynthesis (Ag) estimates between the two models. To this aim we ran again the basic water balance model on all the forest plots but using the estimated parameters instead of the default values.

The following plots show the effect of the new parameters on annual E and annual Ag for plant cohorts of the plots included in the study:

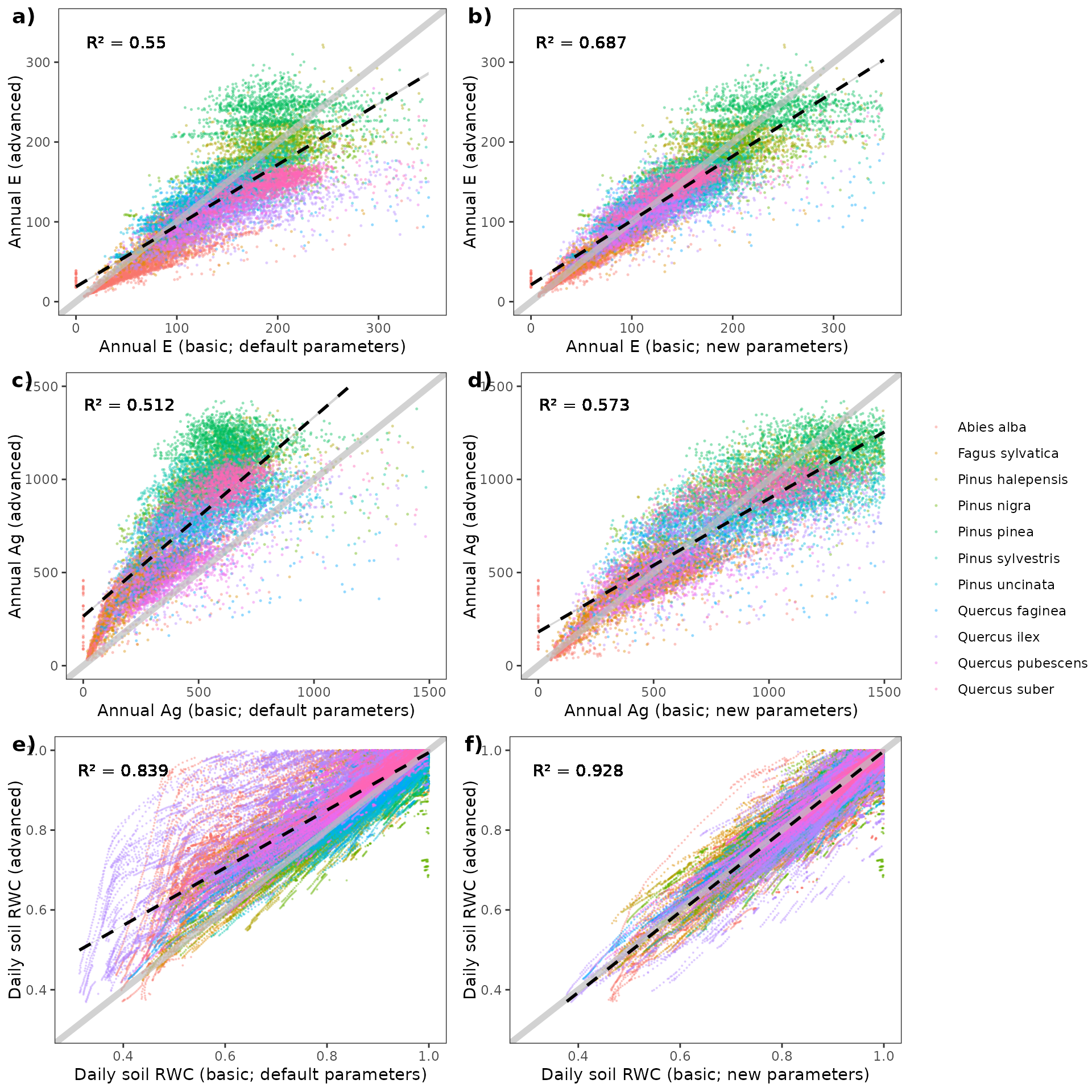
Meta-modelling results for other datasets

The same procedure has been used to estimate Granier’s parameters in the case of the species parameter table SpParamsES, intended to be used for simulations across Spain and distributed using package traits4models. In this case, additional tree species are included, because they are often found in Spain but only seldom in Catalonia. The table containing the five parameters estimated via meta-modelling for SpParamsES is the following:

Name	Tmax_LAI	Tmax_LAIsq	Psi_Extract	Exp_Extract	WUE	WUE_par	WUE_co2	WUE_vpd
Abies alba	0.0684435	-0.0030646	-2.4117055	2.461163	10.647473	0.0811000	0.0028847	-0.2621558
Castanea sativa	0.2299171	-0.0102948	-1.9151784	1.349133	3.965938	0.0467476	0.0025497	-0.4813172
Eucalyptus globulus	0.0659329	-0.0029522	-1.4106981	1.735249	12.834954	0.0549993	0.0024851	-0.6650331
Fagus sylvatica	0.1144470	-0.0051245	-1.5738184	1.531656	8.818881	0.1841914	0.0026525	-0.1814368
Pinus halepensis	0.1295697	-0.0058016	-0.7735734	15.117308	10.317889	0.2443110	0.0021391	-0.5279217
Pinus nigra	0.1459258	-0.0065340	-1.6659657	1.508367	7.668740	0.1291524	0.0030264	-0.5033021
Pinus radiata	0.1069460	-0.0047886	-2.1503247	2.210450	8.540821	0.1262097	0.0036643	-0.4628498
Pinus sylvestris	0.1111574	-0.0049772	-1.5467955	2.732215	9.214660	0.1591069	0.0029310	-0.4333924
Pinus pinaster	0.1666719	-0.0074629	-2.0637003	2.105126	6.748020	0.0912319	0.0021488	-0.5235613
Pinus pinea	0.1546601	-0.0069251	-0.9565976	4.622511	9.290184	0.2249189	0.0021377	-0.5952773
Pinus uncinata	0.1288259	-0.0057683	-2.0344815	1.786279	7.495838	0.1162167	0.0036965	-0.1908863
Quercus faginea	0.2115261	-0.0094713	-1.4969646	1.870994	5.837077	0.0612326	0.0017731	-0.4780129
Quercus ilex ssp. ballota	0.2364658	-0.0105880	-2.4340139	1.436129	4.857045	0.0586140	0.0020683	-0.5387930
Quercus robur	0.2503725	-0.0112107	-1.6676263	2.611057	6.057327	0.0981019	0.0021505	-0.5196672
Quercus pubescens (Q. humilis)	0.3373001	-0.0151030	-1.7699035	2.541723	5.071709	0.0369368	0.0014863	-0.3892295
Quercus suber	0.3953411	-0.0177018	-2.7236054	2.564987	4.399153	0.1167523	0.0017575	-0.5164312

References

De Cáceres M, Molowny-Horas R, Cabon A, Martínez-Vilalta J, Mencuccini M, García-Valdés R, Nadal-Sala D, Sabaté S, Martin-StPaul N, Morin X, D’Adamo F, Batllori E, Améztegui A (2023) MEDFATE 2.9.3: A trait-enabled model to simulate Mediterranean forest function and dynamics at regional scales. Geoscientific Model Development 16, 3165–3201 (https://doi.org/10.5194/gmd-16-3165-2023).
Medrano, H., A. Pou, M. Tomás, S. Martorell, J. Gulias, J. Flexas, and J. M. Escalona. 2012. Average daily light interception determines leaf water use efficiency among different canopy locations in grapevine. Agricultural Water Management 114:4–10.

Miquel De Cáceres

2024-11-05