Understanding model inputs

About this article

Any process-based model of forest functioning and dynamics needs information on climate, vegetation and soils of the forest stand to be simulated. Moreover, since medfate allows simulating cohorts belonging to different species, species-specific parameters are also needed. Finally, simulation control parameters may need to be changed, depending on the goals of the simulation. This article explains data structures required as input to run simulations using the package so that the user can understand them. A companion article Preparing model inputs provides a practical example to illustrate how to create model inputs and some common problems encountered.

Species parameter tables

Simulation models in medfate require a data frame with species (taxon) parameter values. The package includes a default data sets to be readily used. The values of the parameter table were obtained from global trait data bases, bibliographic searches, fit to empirical data or expert-based guesses:

data("SpParamsMED") # For the Spanish forest inventory (including taxon groups)

A large number of parameters (columns) can be found in species parameter tables. Not all parameters are needed for all models. You can find parameter definitions in table SpParamsDefinition, which we reproduce below:

ParameterName	Definition	Type	Units	Strict
Name	Plant names (species binomials, genus or other) used in vegetation data	String	NA	TRUE
SpIndex	Internal species codification (0,1,2,)	Integer	NA	TRUE
AcceptedName	Accepted scientific name of a taxon (genus, species, subspecies or variety) used for parameterization	String	NA	FALSE
Species	Taxonomic species of accepted name	String	NA	FALSE
Genus	Taxonomic genus of accepted name	String	NA	TRUE
Family	Taxonomic family of accepted name	String	NA	TRUE
Order	Taxonomic order of accepted name	String	NA	TRUE
Group	Either “Gymnosperm” or “Angiosperm”	String	NA	TRUE
GrowthForm	Growth form: Either “Shrub”, “Tree” or “Tree/Shrub”	String	Categorical	TRUE
LifeForm	Raunkiaer life form	String	Categorical	TRUE
LeafShape	Broad/Needle/Linear/Scale/Spines/Succulent	String	Categorical	TRUE
LeafSize	Either “Small” (< 225 mm), “Medium” (> 225 mm & < 2025 mm) or “Large” (> 2025 mm)	String	Categorical	TRUE
PhenologyType	Leaf phenology type, either “oneflush-evergreen” (new leaves develop in spring-summer), “progressive-evergreen” (new leaves develop during any season), “winter-deciduous” (leaf senescence in autumn, new leaves in spring-summer) or “winter-semideciduous” (same as before, but abscission of senescent leaves occurs when new leaves are produced).	String	Categorical	TRUE
DispersalType	Dispersal type, either wind-dispersed or animal-dispersed	String	Categorical	TRUE
Hmed	Median plant height	Numeric	cm	TRUE
Hmax	Maximum plant height	Numeric	cm	TRUE
Dmax	Maximum tree diameter	Numeric	cm	FALSE
Z50	Depth corresponding to 50% of fine roots	Numeric	mm	FALSE
Z95	Depth corresponding to 95% of fine roots	Numeric	mm	TRUE
fHDmin	Minimum value of height-diameter ratio	Numeric	NA	FALSE
fHDmax	Maximum value of height-diameter ratio	Numeric	NA	FALSE
a_ash	Allometric coefficient for shrub area as function of height	Numeric	NA	FALSE
b_ash	Allometric coefficient for shrub area as function of height	Numeric	NA	FALSE
a_bsh	Allometric coefficient for fine fuel shrub biomass (dry weight)	Numeric	NA	FALSE
b_bsh	Allometric coefficient for fine fuel shrub biomass (dry weight)	Numeric	NA	FALSE
a_btsh	Allometric coefficient for total fuel shrub biomass (dry weight)	Numeric	NA	FALSE
b_btsh	Allometric coefficient for total fuel shrub biomass (dry weight)	Numeric	NA	FALSE
cr	Proportion of total height corresponding to the crown (i.e. Crown length divided by total height)	Numeric	[0-1]	FALSE
BTsh	Shrub bark thickness	Numeric	mm	FALSE
a_fbt	Regression coefficient for tree foliar biomass	Numeric	NA	FALSE
b_fbt	Regression coefficient for tree foliar biomass	Numeric	NA	FALSE
c_fbt	Regression coefficient for tree foliar biomass	Numeric	NA	FALSE
a_cr	Regression coefficient for crown ratio	Numeric	NA	FALSE
b_1cr	Regression coefficient for crown ratio	Numeric	NA	FALSE
b_2cr	Regression coefficient for crown ratio	Numeric	NA	FALSE
b_3cr	Regression coefficient for crown ratio	Numeric	NA	FALSE
c_1cr	Regression coefficient for crown ratio	Numeric	NA	FALSE
c_2cr	Regression coefficient for crown ratio	Numeric	NA	FALSE
a_cw	Regression coefficient for crown width	Numeric	NA	FALSE
b_cw	Regression coefficient for crown width	Numeric	NA	FALSE
a_bt	Regression coefficient for bark thickness (mm) as function of DBH (cm)	Numeric	NA	FALSE
b_bt	Regression coefficient for bark thickness (mm) as function of DBH (cm)	Numeric	NA	FALSE
LeafDuration	Duration of leaves in year	Numeric	years	FALSE
t0gdd	Date to start the accumulation of degree days	Numeric	days	FALSE
Sgdd	Degree days for leaf budburst	Numeric	Degrees C	FALSE
Tbgdd	Base temperature for the calculation of degree days to leaf budburst	Numeric	Degrees C	FALSE
Ssen	Degree days corresponding to senescence	Numeric	Degrees C	FALSE
Phsen	Photoperiod corresponding to start counting senescence	Numeric	hours	FALSE
Tbsen	Base temperature for the calculation of degree days to senescence	Numeric	Degrees C	FALSE
xsen	Discrete values, to allow for any absent/proportional/more than proportional effects of temperature on senescence	Integer	{0,1,2}	FALSE
ysen	Discrete values, to allow for any absent/proportional/more than proportional effects of photoperiod on senescence	Integer	{0,1,2}	FALSE
SLA	Specific leaf area (mm2/mg = m2/kg)	Numeric	m2/kg	FALSE
LeafDensity	Density of leaf tissue (dry weight over volume)	Numeric	g/cm3	FALSE
WoodDensity	Wood tissue density (at 0% humidity!)	Numeric	g/cm3	FALSE
FineRootDensity	Density of fine root tissue (dry weight over volume).	Numeric	g/cm3	FALSE
conduit2sapwood	Proportion of sapwood corresponding to conducive elements (vessels or tracheids) as opposed to parenchymatic tissue.	Numeric	[0,1]	FALSE
r635	Ratio of foliar (photosynthetic) + small branches (<6.35 mm) dry biomass to foliar (photosynthetic) dry biomass	Numeric	>=1	FALSE
pDead	Proportion of total fine fuels that are dead	Numeric	[0,1]	FALSE
Al2As	Leaf area to sapwood area ratio	Numeric	m2 / m2	FALSE
Ar2Al	Root area to leaf area ratio	Numeric	m2 / m2	FALSE
LeafWidth	Leaf width	Numeric	cm	FALSE
SRL	Specific root length	Numeric	cm/g	FALSE
RLD	Fine root length density (density of root length per soil volume)	Numeric	cm/cm3	FALSE
maxFMC	Maximum fuel moisture (in percent of dry weight)	Numeric	%	FALSE
minFMC	Minimum fuel moisture (in percent of dry weight)	Numeric	%	FALSE
LeafPI0	Osmotic potential at full turgor of leaves	Numeric	Mpa	FALSE
LeafEPS	Modulus of elasticity (capacity of the cell wall to resist changes in volume in response to changes in turgor) of leaves	Numeric	Mpa	FALSE
LeafAF	Apoplastic fraction (proportion of water outside the living cells) in leaves	Numeric	%	FALSE
StemPI0	Osmotic potential at full turgor of symplastic xylem tissue	Numeric	Mpa	FALSE
StemEPS	Modulus of elasticity (capacity of the cell wall to resist changes in volume in response to changes in turgor) of symplastic xylem tissue	Numeric	Mpa	FALSE
StemAF	Apoplastic fraction (proportion of water outside the living cells) in stem xylem	Numeric	%	FALSE
SAV	Surface-area-to-volume ratio of the small fuel (1h) fraction (leaves and branches < 6.35mm)	Numeric	m2/m3	FALSE
HeatContent	High fuel heat content	Numeric	kJ/kg	FALSE
LigninPercent	Percent of lignin+cutin over dry weight in leaves	Numeric	%	FALSE
LeafAngle	The angle between the leaf plane and the horizontal plane (i.e. leaf zenith angle)	Numeric	degrees	FALSE
LeafAngleSD	Standard deviation of the leaf angle	Numeric	degrees	FALSE
ClumpingIndex	Canopy clumping index	Numeric	[0-1]	FALSE
gammaSWR	Reflectance (albedo) coefficient for SWR (gammaPAR is 0.8*gammaSWR)	Numeric	unitless	FALSE
alphaSWR	Absorbance coefficient for SWR (alphaPAR is alphaSWR*1.35)	Numeric	unitless	FALSE
kPAR	Light extinction coeficient for PAR (extinction coefficient for SWR is kPAR/1.35)	Numeric	unitless	FALSE
g	Canopy water storage capacity per LAI unit	Numeric	mm/LAI	FALSE
Tmax_LAI	Empirical coefficient relating LAI with the ratio of maximum transpiration over potential evapotranspiration.	Numeric	NA	FALSE
Tmax_LAIsq	Empirical coefficient relating squared LAI with the ratio of maximum transpiration over potential evapotranspiration.	Numeric	NA	FALSE
Psi_Extract	Water potential corresponding to 50% reduction of transpiration	Numeric	MPa	FALSE
Exp_Extract	Parameter of the Weibull function regulating transpiration reduction	Numeric	NA	FALSE
WUE	Daily water use efficiency (gross photosynthesis over transpiration) under no light, water or CO2 limitations and VPD = 1kPa	Numeric	g C * mm H2O-1	FALSE
WUE_par	Coefficient regulating the influence of % PAR on gross photosynthesis	Numeric	NA	FALSE
WUE_co2	Coefficient regulating the influence of atmospheric CO2 concentration on gross photosynthesis	Numeric	NA	FALSE
WUE_vpd	Coefficient regulating the influence of vapor pressure deficit (VPD) on gross photosynthesis	Numeric	NA	FALSE
Gswmin	Minimum leaf conductance (cuticular+incomplete closure) at 20C	Numeric	mol H2O * s-1 * m-2	FALSE
Gswmax	Maximum stomatal conductance to water vapour	Numeric	mol H2O * s-1 * m-2	FALSE
Gsw_AC_slope	Slope of the Gsw vs Ac/Cs relationship (Baldocchi model).	Numeric	mol H2O * mmol CO2-1	FALSE
Gs_Toptim	Temperature corresponding to maximal stomatal conductance	Numeric	Degrees C	FALSE
Gs_Tsens	Stomatal sensitivity to temperature	Numeric	NA	FALSE
Gs_P50	Water potential causing 50% reduction in stomatal conductance	Numeric	MPa	FALSE
Gs_slope	Rate of decrease in stomatal conductance at Gs_P50	Numeric	%/MPa	FALSE
VCleaf_kmax	Maximum leaf hydraulic conductance	Numeric	mmol H2O * s-1 * m-2 * MPa-1	FALSE
VCleaf_P12	12% of maximum conductance of the leaf vulnerability curve	Numeric	MPa	FALSE
VCleaf_P50	50% of maximum conductance of the leaf vulnerability curve	Numeric	MPa	FALSE
VCleaf_P88	88% of maximum conductance of the leaf vulnerability curve	Numeric	MPa	FALSE
VCleaf_slope	Slope of the rate of leaf embolism spread at VCleaf_P50	Numeric	%/MPa	FALSE
Kmax_stemxylem	Maximum sapwood-specific hydraulic conductivity of stem xylem	Numeric	kg H2O * s-1 * m-1 * Mpa-1	FALSE
VCstem_P12	12% of maximum conductance of the stem vulnerability curve	Numeric	MPa	FALSE
VCstem_P50	50% of maximum conductance of the stem vulnerability curve	Numeric	MPa	FALSE
VCstem_P88	88% of maximum conductance of the stem vulnerability curve	Numeric	MPa	FALSE
VCstem_slope	Slope of the rate of stem embolism spread at VCleaf_P50	Numeric	%/MPa	FALSE
Kmax_rootxylem	Maximum sapwood-specific hydraulic conductivity of root xylem	Numeric	kg H2O * s-1 * m-1 * Mpa-1	FALSE
VCroot_P12	12% of maximum conductance of the root vulnerability curve	Numeric	MPa	FALSE
VCroot_P50	50% of maximum conductance of the root vulnerability curve	Numeric	MPa	FALSE
VCroot_P88	88% of maximum conductance of the root vulnerability curve	Numeric	MPa	FALSE
VCroot_slope	Slope of the rate of root embolism spread at VCleaf_P50	Numeric	%/MPa	FALSE
Vmax298	Maximum Rubisco carboxilation rate	Numeric	mmol CO2 * s-1* m-2	FALSE
Jmax298	Maximum rate of electron transport at 298K	Numeric	mmol electrons * s-1 * m-2	FALSE
Nleaf	Nitrogen mass per leaf dry mass	Numeric	mg N / g dry	FALSE
Nsapwood	Nitrogen mass per sapwood dry mass	Numeric	mg N / g dry	FALSE
Nfineroot	Nitrogen mass per fine root dry mass	Numeric	mg N / g dry	FALSE
WoodC	Wood carbon content per dry mass	Numeric	g C / g dry	FALSE
RERleaf	Maintenance respiration rates for leaves.	Numeric	g gluc * g dry-1 * day-1	FALSE
RERsapwood	Maintenance respiration rates for living cells of sapwood.	Numeric	g gluc * g dry-1 * day-1	FALSE
RERfineroot	Maintenance respiration rates for fine roots.	Numeric	g gluc * g dry-1 * day-1	FALSE
CCleaf	Leaf construction costs	Numeric	g gluc * g dry-1	FALSE
CCsapwood	Sapwood construction costs	Numeric	g gluc * g dry-1	FALSE
CCfineroot	Fine root construction costs	Numeric	g gluc * g dry-1	FALSE
RGRleafmax	Maximum leaf relative growth rate	Numeric	m2/cm2/day	FALSE
RGRsapwoodmax	Maximum sapwood growth rate relative to sapwood area (for shrubs)	Numeric	cm2/cm2/day	FALSE
RGRcambiummax	Maximum sapwood growth rate relative to cambium perimeter (for trees)	Numeric	cm2/cm/day	FALSE
RGRfinerootmax	Maximum fineroot relative growth rate	Numeric	g dry/g dry/day	FALSE
SRsapwood	Sapwood daily senescence rate	Numeric	Day-1	FALSE
SRfineroot	Fine root daily senescence rate	Numeric	Day-1	FALSE
RSSG	Minimum relative starch for sapwood growth	Numeric	[0-1]	FALSE
MortalityBaselineRate	Deterministic proportion or probability specifying the baseline reduction of cohort’s density occurring in a year	Numeric	Year-1	FALSE
SurvivalModelStep	Time step in years of the empirical survival model depending on stand basal area (e.g. 10)	Numeric	Year	FALSE
SurvivalB0	Intercept of the logistic baseline survival model depending on stand basal area	Numeric	NA	FALSE
SurvivalB1	Slope of the logistic baseline survival model depending on stand basal area	Numeric	NA	FALSE
SeedProductionHeight	Minimum shrub height for seed production	Numeric	cm	FALSE
SeedProductionDiameter	Minimum tree diameter for seed production	Numeric	cm	FALSE
SeedMass	Seed dry mass	Numeric	mg	FALSE
SeedLongevity	Seedbank average longevity	Numeric	yr	FALSE
DispersalDistance	Distance parameter for dispersal kernel	Numeric	m	FALSE
DispersalShape	Shape parameter for dispersal kernel	Numeric	NA	FALSE
ProbRecr	Probability of recruitment within the bioclimatic envelope	Numeric	[0-1]	FALSE
MinTempRecr	Minimum average temperature of the coldest month for successful recruitment	Numeric	Degrees C	FALSE
MinMoistureRecr	Minimum value of the moisture index (annual precipitation over annual PET) for successful recruitment	Numeric	unitless	FALSE
MinFPARRecr	Minimum percentage of PAR at the ground level for successful recruitment	Numeric	%	FALSE
RecrTreeDBH	Recruitment tree dbh (typically 1 cm)	Numeric	cm	FALSE
RecrTreeHeight	Recruitment tree (sapling) height	Numeric	cm	FALSE
RecrShrubHeight	Recruitment shrub height	Numeric	cm	FALSE
RecrTreeDensity	Recruitment tree (sapling) density	Numeric	ind/ha	FALSE
RecrShrubCover	Recruitment shrub cover	Numeric	%	FALSE
RecrZ50	Recruitment depth corresponding to 50% of fine roots	Numeric	mm	FALSE
RecrZ95	Recruitment depth corresponding to 95% of fine roots	Numeric	mm	FALSE
RespFire	Probability of resprouting after fire disturbance	Numeric	[0-1]	FALSE
RespDist	Probability of resprouting after undefined disturbance (typically desiccation)	Numeric	[0-1]	FALSE
RespClip	Probability of resprouting after clipping	Numeric	[0-1]	FALSE
IngrowthTreeDensity	Tree density when reaching DBH of ingrowth	Numeric	cm	FALSE
IngrowthTreeDBH	Tree DBH of ingrowth (typically 7.5 cm)	Numeric	ind/ha	FALSE

In order to understand the role of parameters in the model, you should read the details of model design and formulation included in the medfatebook. Details regarding how the species parameter tables are build can be found in traits4models.

Vegetation

Forest objects

Models included in medfate were primarily designed to be ran on forest inventory plots. In this kind of data, the vegetation of a sampled area is often described by several records of woody plants (trees and shrubs) along with their size and species identity. Forest plots in medfate are assumed to be in a data structure that follows closely the Spanish national forest inventory, but is simple enough to so that other forest sampling schemes can be mapped onto it.

Each forest plot is represented in an object of class forest, a list that contains several elements. Among them, the most important items are two data frames, treeData (for trees) and shrubData (for shrubs):

data(exampleforest)
exampleforest

## $treeData
##            Species   N   DBH Height Z50  Z95
## 1 Pinus halepensis 168 37.55    800 100  600
## 2     Quercus ilex 384 14.60    660 300 1000
## 
## $shrubData
##             Species Cover Height Z50  Z95
## 1 Quercus coccifera  3.75     80 200 1000
## 
## $herbCover
## [1] 10
## 
## $herbHeight
## [1] 20
## 
## $seedBank
## [1] Species Percent
## <0 rows> (or 0-length row.names)
## 
## attr(,"class")
## [1] "forest" "list"

Trees are expected to be primarily described in terms of species, diameter (DBH; cm) and height (cm), whereas shrubs are described in terms of species, percent cover (%) and mean height (cm). Root distribution has to be specified for both growth forms, in terms of the depths (mm) corresponding to 50% and 95% of cumulative fine root distribution. Functions are provided in the package to map variables in user data frames into tables treeData and shrubData. Information about the herb layer may be either absent or included in an aggregated way (i.e. without distinguishing cohorts).

While the former example illustrates the standard structure of a forest object, users may use an alternative description, based on leaf area index and crown ratio of woody cohorts and the herb layer:

data(exampleforest2)
exampleforest2

## $treeData
##            Species  N DBH Height Z50  Z95 LAI CrownRatio
## 1 Pinus halepensis NA  NA    800 100  600 0.8       0.66
## 2     Quercus ilex NA  NA    660 300 1000 0.5       0.60
## 
## $shrubData
##             Species Cover Height Z50  Z95  LAI CrownRatio
## 1 Quercus coccifera    NA     80 200 1000 0.03        0.8
## 
## $herbCover
## [1] NA
## 
## $herbHeight
## [1] 20
## 
## $herbLAI
## [1] 0.25
## 
## $seedBank
## [1] Species Percent
## <0 rows> (or 0-length row.names)
## 
## attr(,"class")
## [1] "forest" "list"

This alternative forest form is suitable for water balance simulations, but does not allow simulating forest dynamics.

Single-cohort forests

Although medfate has been designed to perform simulations on multi-cohort forests, it can also handle simulations where vegetation is described using a single cohort. Functions tree2forest() and shrub2forest() allow defining single-cohort forests from attributes. For example a holm oak (Quercus ilex) forest of 4-m height and having a leaf area index of $2\, m^2\cdot m^{-2}$ can be defined using:

oak_forest <-tree2forest("Quercus ilex", Height= 400, LAI = 2)

The function will return a forest object where most attributes are empty:

oak_forest

## $treeData
##        Species DBH Height  N Z50 Z95 LAI
## 1 Quercus ilex  NA    400 NA  NA  NA   2
## 
## $shrubData
## [1] Species Height  Cover   Z50     Z95    
## <0 rows> (or 0-length row.names)
## 
## $herbCover
## [1] NA
## 
## $herbHeight
## [1] NA
## 
## $seedBank
## [1] Species Percent
## <0 rows> (or 0-length row.names)
## 
## attr(,"class")
## [1] "forest" "list"

Since density and diameter have not been provided, simulations in this case will be restricted to water balance. Moreover, note that when defining single-cohort forests all possible interactions with functionally distinct plants are neglected.

Aboveground and belowground data

We can use some functions to inspect how above-ground and below-ground information is represented in medfate.

For example, we can use function forest2aboveground() on the object exampleforest to show how medfate completes above-ground information:

above <- forest2aboveground(exampleforest, SpParamsMED)
above

##         SP        N   DBH Cover   H        CR   LAI_live LAI_expanded LAI_dead
## T1_148 148 168.0000 37.55    NA 800 0.6605196 0.84874773   0.84874773        0
## T2_168 168 384.0000 14.60    NA 660 0.6055642 0.70557382   0.70557382        0
## S1_165 165 749.4923    NA  3.75  80 0.8032817 0.03062604   0.03062604        0
##        LAI_nocomp ObsID
## T1_148 1.29720268  <NA>
## T2_168 1.01943205  <NA>
## S1_165 0.04412896  <NA>

Note that the call to forest2aboveground() included the species parameter table, because species-specific allometric coefficients are needed to calculate leaf area from tree size or shrub percent cover and height. Moreover, note that the plant cohorts were given unique codes that tell us whether they correspond to trees (‘T’) or shrubs (‘S’).

Columns N, DBH and Cover describe forest structure and are required for simulating growth, but not for soil water balance, which only requires columns SP, H (in cm), CR (i.e. the crown ratio), LAI_live, LAI_expanded and LAI_dead. Therefore, one could use alternative forest description as starting point, i.e.:

above2 <- forest2aboveground(exampleforest2, SpParamsMED)
above2

##         SP  N DBH Cover   H   CR LAI_live LAI_expanded LAI_dead LAI_nocomp
## T1_148 148 NA  NA    NA 800 0.66     0.80         0.80        0       0.80
## T2_168 168 NA  NA    NA 660 0.60     0.50         0.50        0       0.50
## S1_165 165 NA  NA    NA  80 0.80     0.03         0.03        0       0.03
##        ObsID
## T1_148  <NA>
## T2_168  <NA>
## S1_165  <NA>

Of course, the resulting data frame has missing values, whereas the other values are directly copied from forest.

Aboveground leaf area distribution (with or without distinguishing among cohorts) can be examined by calling function vprofile_leafAreaDensity():

vprofile_leafAreaDensity(exampleforest, SpParamsMED, byCohorts = F)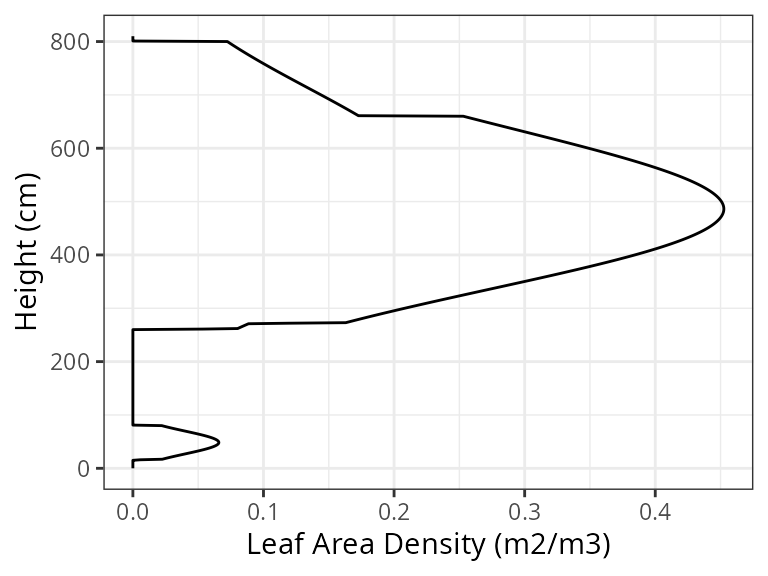

Leaf area density plot

vprofile_leafAreaDensity(exampleforest, SpParamsMED, byCohorts = T)

Leaf area density plot by species

Belowground data

Regarding belowground information, we need vectors with depths corresponding to 50% and 95% of fine roots, which we simply concatenate from our forest data:

Z50 <- c(exampleforest$treeData$Z50, exampleforest$shrubData$Z50)
Z95 <- c(exampleforest$treeData$Z95, exampleforest$shrubData$Z95)

These parameters specify a continuous distribution of fine roots. Users can visually inspect the distribution of fine roots of forest objects by calling function vprofile_rootDistribution():

vprofile_rootDistribution(exampleforest, SpParamsMED)

Fine root distribution

Soils

Soil physical description

Simulation models in medfate require information on the physical attributes of soil, namely soil depth, texture, bulk density and rock fragment content. Soil physical attributes can be initialized to default values, for a given number of layers, using function defaultSoilParams():

spar <- defaultSoilParams(4)
print(spar)

##   widths clay sand om nitrogen  bd rfc
## 1    300   25   25 NA       NA 1.5  25
## 2    700   25   25 NA       NA 1.5  45
## 3   1000   25   25 NA       NA 1.5  75
## 4   2000   25   25 NA       NA 1.5  95

where widths are soil layer widths in mm; clay and sand are the percentage of clay and sand, in percent of dry weight, om stands for organic matter, bd is bulk density (in $g \cdot cm^{-3}$ ) and rfc the percentage of rock fragments. Because soil properties vary strongly at fine spatial scales, ideally soil physical attributes should be measured on samples taken at the forest stand to be simulated. For those users lacking such data, soil properties are available via SoilGrids.org.

Initialized soil object

Simulations need additional soil parameters and state variables. The soil input for simulations is an object of class soil (also a data frame) that is created using a function with the same name:

examplesoil <- soil(spar)
class(examplesoil)

## [1] "soil"       "data.frame"

In addition to the physical soil description, this object contains soil parameters and state variables needed for soil water balance simulations:

examplesoil

##   widths sand clay      usda om nitrogen  bd rfc  macro     Ksat VG_alpha
## 1    300   25   25 Silt loam NA       NA 1.5  25 0.0485 5401.471 89.16112
## 2    700   25   25 Silt loam NA       NA 1.5  45 0.0485 5401.471 89.16112
## 3   1000   25   25 Silt loam NA       NA 1.5  75 0.0485 5401.471 89.16112
## 4   2000   25   25 Silt loam NA       NA 1.5  95 0.0485 5401.471 89.16112
##       VG_n VG_theta_res VG_theta_sat W Temp
## 1 1.303861        0.041     0.423715 1   NA
## 2 1.303861        0.041     0.423715 1   NA
## 3 1.303861        0.041     0.423715 1   NA
## 4 1.303861        0.041     0.423715 1   NA

For example, macro specifies the macroporosity of each layer. The meaning of all elements in the soil object can be found in the help page for function soil().

At any time, one can show the characteristics and status of the soil object using its summary function:

summary(examplesoil, model = "SX")

## Soil depth (mm): 4000 
## 
## Layer  1  [ 0  to  300 mm ] 
##     clay (%): 25 silt (%): 50 sand (%): 25 organic matter (%): NA [ Silt loam ]
##     Rock fragment content (%): 25 Macroporosity (%): 5 
##     Theta WP (%): 14 Theta FC (%): 30 Theta SAT (%): 49 Theta current (%) 30 
##     Vol. WP (mm): 32 Vol. FC (mm): 68 Vol. SAT (mm): 111 Vol. current (mm): 68 
##     Temperature (Celsius): NA 
## 
## Layer  2  [ 300  to  1000 mm ] 
##     clay (%): 25 silt (%): 50 sand (%): 25 organic matter (%): NA [ Silt loam ]
##     Rock fragment content (%): 45 Macroporosity (%): 5 
##     Theta WP (%): 14 Theta FC (%): 30 Theta SAT (%): 49 Theta current (%) 30 
##     Vol. WP (mm): 55 Vol. FC (mm): 117 Vol. SAT (mm): 190 Vol. current (mm): 117 
##     Temperature (Celsius): NA 
## 
## Layer  3  [ 1000  to  2000 mm ] 
##     clay (%): 25 silt (%): 50 sand (%): 25 organic matter (%): NA [ Silt loam ]
##     Rock fragment content (%): 75 Macroporosity (%): 5 
##     Theta WP (%): 14 Theta FC (%): 30 Theta SAT (%): 49 Theta current (%) 30 
##     Vol. WP (mm): 36 Vol. FC (mm): 76 Vol. SAT (mm): 123 Vol. current (mm): 76 
##     Temperature (Celsius): NA 
## 
## Layer  4  [ 2000  to  4000 mm ] 
##     clay (%): 25 silt (%): 50 sand (%): 25 organic matter (%): NA [ Silt loam ]
##     Rock fragment content (%): 95 Macroporosity (%): 5 
##     Theta WP (%): 14 Theta FC (%): 30 Theta SAT (%): 49 Theta current (%) 30 
##     Vol. WP (mm): 14 Vol. FC (mm): 30 Vol. SAT (mm): 49 Vol. current (mm): 30 
##     Temperature (Celsius): NA 
## 
## Total soil saturated capacity (mm): 473 
## Total soil water holding capacity (mm): 291 
## Total soil extractable water (mm): 183 
## Total soil current Volume (mm): 291 
## Saturated water depth (mm): NA

Importantly, the soil object is used to store the degree of moisture of each soil layer. In particular, element W contains the state variable that represents moisture content - the proportion of moisture relative to field capacity - which is normally initialized to 1 for each layer:

examplesoil$W

## [1] 1 1 1 1

Advanced soil plant energy and water balance modelling requires considering the temperature of soil. Hence, Temp contains the temperature (in degrees) of soil layers:

examplesoil$Temp

## [1] NA NA NA NA

Soil layer temperatures are initialized to missing values, so that at the first time step they will be set to atmospheric temperature. While simple water balance modeling can be run using either Saxton’s or Van Genuchten’s equations as water retention curves, Van Genuchten’s model is forced for advanced modelling.

Users can skip the call function soil() when creating input objects for simulations (see below).

Water retention curves

The modelled moisture content of the soil depends on the water retention curve used to represent the relationship between soil volumetric water content ( $\theta$ ; %) and soil water potential ( $\Psi$ ; MPa). By default the Saxton (model = "SX") equations are used to model the water retention curve, but the user may choose to follow Van Genuchten - Mualem equations, which will give slightly different values for the same texture:

summary(examplesoil, model="VG")

## Soil depth (mm): 4000 
## 
## Layer  1  [ 0  to  300 mm ] 
##     clay (%): 25 silt (%): 50 sand (%): 25 organic matter (%): NA [ Silt loam ]
##     Rock fragment content (%): 25 Macroporosity (%): 5 
##     Theta WP (%): 13 Theta FC (%): 30 Theta SAT (%): 42 Theta current (%) 30 
##     Vol. WP (mm): 29 Vol. FC (mm): 68 Vol. SAT (mm): 95 Vol. current (mm): 68 
##     Temperature (Celsius): NA 
## 
## Layer  2  [ 300  to  1000 mm ] 
##     clay (%): 25 silt (%): 50 sand (%): 25 organic matter (%): NA [ Silt loam ]
##     Rock fragment content (%): 45 Macroporosity (%): 5 
##     Theta WP (%): 13 Theta FC (%): 30 Theta SAT (%): 42 Theta current (%) 30 
##     Vol. WP (mm): 49 Vol. FC (mm): 117 Vol. SAT (mm): 163 Vol. current (mm): 117 
##     Temperature (Celsius): NA 
## 
## Layer  3  [ 1000  to  2000 mm ] 
##     clay (%): 25 silt (%): 50 sand (%): 25 organic matter (%): NA [ Silt loam ]
##     Rock fragment content (%): 75 Macroporosity (%): 5 
##     Theta WP (%): 13 Theta FC (%): 30 Theta SAT (%): 42 Theta current (%) 30 
##     Vol. WP (mm): 32 Vol. FC (mm): 76 Vol. SAT (mm): 106 Vol. current (mm): 76 
##     Temperature (Celsius): NA 
## 
## Layer  4  [ 2000  to  4000 mm ] 
##     clay (%): 25 silt (%): 50 sand (%): 25 organic matter (%): NA [ Silt loam ]
##     Rock fragment content (%): 95 Macroporosity (%): 5 
##     Theta WP (%): 13 Theta FC (%): 30 Theta SAT (%): 42 Theta current (%) 30 
##     Vol. WP (mm): 13 Vol. FC (mm): 30 Vol. SAT (mm): 42 Vol. current (mm): 30 
##     Temperature (Celsius): NA 
## 
## Total soil saturated capacity (mm): 407 
## Total soil water holding capacity (mm): 291 
## Total soil extractable water (mm): 194 
## Total soil current Volume (mm): 291 
## Saturated water depth (mm): NA

While Saxton equations use texture and organic matter as inputs, the Van Genuchten-Mualem equations need other parameters, which are estimated using pedotransfer functions and their names start with VG_ (two alternative options are provided in function soil to estimate Van Genuchten parameters). The following code calls function soil_retentionCurvePlot() to illustrate the difference between the two water retention models in this soil:

soil_retentionCurvePlot(examplesoil, model="both")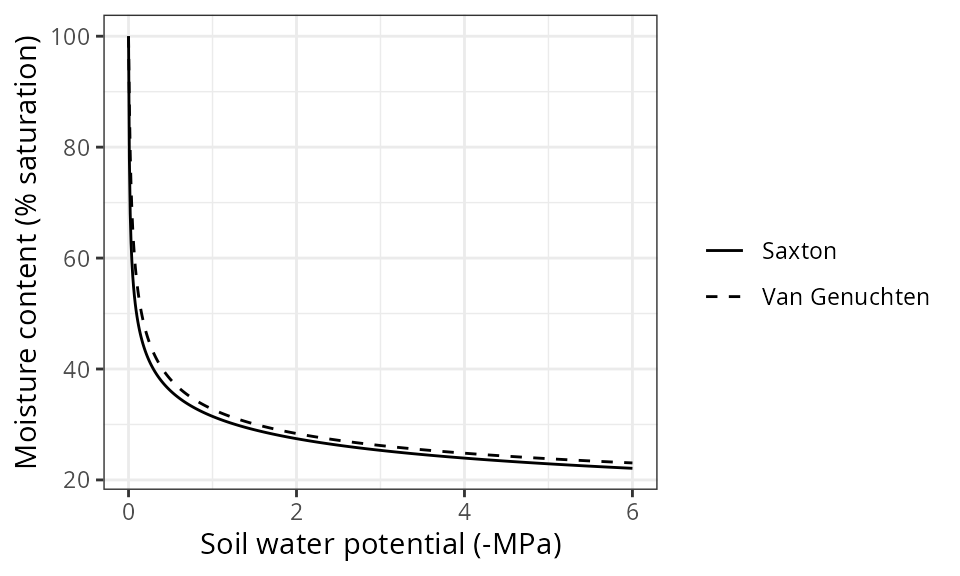

Soil water retention

Low-level functions, such as soil_psi2thetaSX() and soil_psi2thetaVG() (and their counterparts soil_theta2psiSX() and soil_theta2psiVG()), can be used to calculate volumetric soil moisture from the water potential (and viceversa) using the two models. When simulating soil water balance, the user can choose among the two models (see control parameters below).

Meteorological forcing

All simulations in the package require daily weather inputs. The minimum weather variables that are required are minimum/maximum temperature, minimum/maximum relative humidity, precipitation and radiation. Other variables like wind speed are recommended but not required. Here we show an example of meteorological forcing data.

data(examplemeteo)
head(examplemeteo)

##        dates MinTemperature MaxTemperature Precipitation MinRelativeHumidity
## 1 2001-01-01     -0.5934215       6.287950      4.869109            65.15411
## 2 2001-01-02     -2.3662458       4.569737      2.498292            57.43761
## 3 2001-01-03     -3.8541036       2.661951      0.000000            58.77432
## 4 2001-01-04     -1.8744860       3.097705      5.796973            66.84256
## 5 2001-01-05      0.3288287       7.551532      1.884401            62.97656
## 6 2001-01-06      0.5461322       7.186784     13.359801            74.25754
##   MaxRelativeHumidity Radiation WindSpeed
## 1           100.00000  12.89251  2.000000
## 2            94.71780  13.03079  7.662544
## 3            94.66823  16.90722  2.000000
## 4            95.80950  11.07275  2.000000
## 5           100.00000  13.45205  7.581347
## 6           100.00000  12.84841  6.570501

Simulation models in medfate have been designed to work along with data generated from package meteoland. The user is strongly recommended to resort to this package to obtain suitable weather input for medfate simulations.

Simulation control

Apart from data inputs, the behaviour of simulation models can be controlled using a set of global parameters. The default parameterization is obtained using function defaultControl():

control <- defaultControl()
names(control)

##   [1] "fillMissingRootParams"            "fillMissingSpParams"             
##   [3] "fillMissingWithGenusParams"       "verbose"                         
##   [5] "subdailyResults"                  "standResults"                    
##   [7] "soilResults"                      "snowResults"                     
##   [9] "plantResults"                     "plantWaterBalanceResults"        
##  [11] "labileCarbonBalanceResults"       "plantStructureResults"           
##  [13] "growthMortalityResults"           "leafResults"                     
##  [15] "temperatureResults"               "fireHazardResults"               
##  [17] "fireHazardStandardWind"           "fireHazardStandardDFMC"          
##  [19] "transpirationMode"                "soilFunctions"                   
##  [21] "VG_PTF"                           "ndailysteps"                     
##  [23] "max_nsubsteps_soil"               "defaultWindSpeed"                
##  [25] "defaultCO2"                       "defaultRainfallIntensityPerMonth"
##  [27] "leafPhenology"                    "bareSoilEvaporation"             
##  [29] "unlimitedSoilWater"               "interceptionMode"                
##  [31] "infiltrationMode"                 "infiltrationCorrection"          
##  [33] "soilDomains"                      "rhizosphereOverlap"              
##  [35] "unfoldingDD"                      "verticalLayerSize"               
##  [37] "windMeasurementHeight"            "segmentedXylemVulnerability"     
##  [39] "stemCavitationRecovery"           "leafCavitationRecovery"          
##  [41] "lfmcComponent"                    "hydraulicRedistributionFraction" 
##  [43] "nsubsteps_canopy"                 "taper"                           
##  [45] "multiLayerBalance"                "sapFluidityVariation"            
##  [47] "TPhase_gmin"                      "Q10_1_gmin"                      
##  [49] "Q10_2_gmin"                       "rootRadialConductance"           
##  [51] "averageFracRhizosphereResistance" "thermalCapacityLAI"              
##  [53] "boundaryLayerSize"                "cavitationRecoveryMaximumRate"   
##  [55] "sunlitShade"                      "numericParams"                   
##  [57] "leafCavitationEffects"            "stemCavitationEffects"           
##  [59] "stomatalSubmodel"                 "plantCapacitance"                
##  [61] "cavitationFlux"                   "soilDisconnection"               
##  [63] "leafCuticularTranspiration"       "stemCuticularTranspiration"      
##  [65] "C_SApoInit"                       "C_LApoInit"                      
##  [67] "k_SSym"                           "fractionLeafSymplasm"            
##  [69] "gs_NightFrac"                     "JarvisPAR"                       
##  [71] "fTRBToLeaf"                       "subdailyCarbonBalance"           
##  [73] "allowDessication"                 "allowStarvation"                 
##  [75] "sinkLimitation"                   "shrubDynamics"                   
##  [77] "herbDynamics"                     "allocationStrategy"              
##  [79] "phloemConductanceFactor"          "nonSugarConcentration"           
##  [81] "equilibriumOsmoticConcentration"  "minimumRelativeStarchForGrowth"  
##  [83] "constructionCosts"                "senescenceRates"                 
##  [85] "maximumRelativeGrowthRates"       "mortalityMode"                   
##  [87] "mortalityBaselineRate"            "mortalityRelativeSugarThreshold" 
##  [89] "mortalityRWCThreshold"            "recrTreeDBH"                     
##  [91] "recrTreeDensity"                  "ingrowthTreeDBH"                 
##  [93] "ingrowthTreeDensity"              "allowSeedBankDynamics"           
##  [95] "allowRecruitment"                 "allowResprouting"                
##  [97] "recruitmentMode"                  "removeEmptyCohorts"              
##  [99] "minimumTreeCohortDensity"         "minimumShrubCohortCover"         
## [101] "dynamicallyMergeCohorts"          "keepCohortsWithObsID"            
## [103] "seedRain"                         "seedProductionTreeHeight"        
## [105] "seedProductionShrubHeight"        "probRecr"                        
## [107] "minTempRecr"                      "minMoistureRecr"                 
## [109] "minFPARRecr"                      "recrTreeHeight"                  
## [111] "recrShrubCover"                   "recrShrubHeight"                 
## [113] "recrTreeZ50"                      "recrShrubZ50"                    
## [115] "recrTreeZ95"                      "recrShrubZ95"

Control parameters should normally be left to their default value until their effect on simulations is fully understood.

Input objects for simulation functions

Simulation functions spwb() and growth() (and similar functions) require first combining forest, soil, species-parameter and simulation control inputs into a single input object (of class spwbInput or growthInput) that is then used as input to the corresponding simulation function along with weather data. The combination of vegetation, soil and control inputs is done via functions spwbInput() and growthInput(). While it requires one additional line of code, having this additional step is handy because cohort-level parameters and state variables initialized can then be modified by the user (or an automated calibration algorithm) before calling the actual simulation functions. The input objects for functions spwb() and growth() are presented in more detail in articles Basic water balance and Forest growth, respectively.

Function fordyn() is different from the other two simulation functions, in the sense that the user enters forest, soil, species-parameter and simulation control inputs directly into the simulation function (in fact, fordyn() internally calls growthInput() to initialize the input object to function growth()).

Miquel De Caceres

2024-11-05