A Inbuilt parameter estimation

A.1 Introduction

Package medfate has been designed to allow simulations requiring a minimum set of vegetation functional parameters. This entails that several other parameters have to be estimated automatically (via inbuilt procedures) before starting simulations. Inbuilt parameter estimation is done in functions spwbInput() and growthInput(), with the user controlling the process through the species parameter table input (e.g., SpParamsMED) and the object control (see default control values in defaultControl()).

A.2 Strict, scaled and imputable parameters

Different kinds of vegetation functional parameters can be distinguished according to whether inbuilt parameter estimation is possible and how it is conducted:

• Strictly-required parameters are those for which there are no inbuilt estimation procedures implemented in the initialization functions. Hence, either values in the species parameter table input are non-missing or suitable values need to be specified before running simulation models. Since medfate ver. 2.3, only plant/leaf classification parameters and plant size parameters are strict. The remaining ones can be estimated from other parameters. This facilitates having a functional species parameter table, because only a set of parameters have to be strictly filled, from either soft trait databases or forest inventory data.
• Scaled parameters are functional parameters that cannot be defined at the species level, because they need to be estimated taking into account the size and structure of the plant cohort. These are not normally defined at the level of species parameter table. Specific control parameters are used to determine how scaling is performed.
• Imputable parameters parameters are those for which the initialization routines can provide default values or estimations derived from relationships with other parameters. Parameter imputation is conducted if control parameter fillMissingSpParams = TRUE. Sometimes, default parameter values are also specified in the control object.

The following tables describe how the different functional parameters are dealt with, grouped by function. Links are given to the chapter subsections where scaling and/or imputation procedures are described.

Plant/leaf classification

Symbol	R	Description	Strict	Scaled	Imputable
\(GF\)	GrowthForm	Growth form, defined depending on the treatment in forest inventory plots (Tree, Shrub or Tree/Shrub)	Yes	No	No
\(LF\)	LifeForm	Raunkiaer life form	Yes	No	No
\(L_{shape}\)	LeafShape	Leaf type (Linear, Needle, Broad, Scale, Spines or Succulent)	Yes	No	No
\(L_{size}\)	LeafSize	Leaf size (Small, Medium, Large)	Yes	No	No
\(L_{pheno}\)	PhenologyType	Leaf phenology type	Yes	No	No

Plant size

Symbol	R	Description	Strict	Scaled	Imputable
\(H_{max}\)	Hmed	Maximum plant height	Yes	No	No
\(H_{med}\)	Hmed	Median plant height	Yes	No	No
\(Z_{50}\)	Z50	Depth above which 50% of the fine root mass is located	No	No	A.3.1
\(Z_{95}\)	Z95	Depth above which 95% of the fine root mass is located	Yes	No	No

Allometric coefficients

Symbol	R	Description	Strict	Scaled	Imputable
\(a_{ash}\), \(b_{ash}\)	a_ash, b_ash	Coefficients relating the square of shrub height with shrub area	No	No	A.3.2
\(a_{bsh}\), \(b_{bsh}\)	a_bsh, b_bsh	Coefficients relating crown volume with dry weight of shrub individuals	No	No	A.3.2
\(cr\)	cr	Ratio between crown length and total height for shrubs	No	No	A.3.2
\(a_{fbt}\), \(b_{fbt}\), \(c_{fbt}\)	a_fbt, b_fbt, c_fbt	Coefficients to calculate foliar biomass of an individual tree	No	No	A.3.3
\(a_{cr}\), \(b_{1cr}\), \(b_{2cr}\), \(b_{3cr}\), \(c_{1cr}\), \(c_{2cr}\)	a_cr, b_1cr, b_2cr, b_3cr, c_1cr, c_2cr	Coefficients to calculate crown ratio of trees	No	No	A.3.3
\(a_{cw}\), \(b_{cw}\)	a_cw, b_cw	Regression coefficients used to calculate the crown width of trees	No	No	A.3.3
\(f_{HD,min}\)	fHDmin	Minimum height-to-diameter ratio	No	No	A.3.3
\(f_{HD,max}\)	fHDmax	Maximum height-to-diameter ratio	No	No	A.3.3

Leaf phenology

Symbol	R	Description	Strict	Scaled	Imputable
\(LD\)	LeafDuration	Average duration of leaves	No	No	A.3.9
\(t_{0,eco}\)	t0gdd	Degree days corresponding to leaf budburst	No	No	A.3.9
\(S^*_{eco}\)	Sgdd	Degree days corresponding to leaf budburst	No	No	A.3.9
\(T_{eco}\)	Tbgdd	Base temperature for the calculation of degree days to leaf budburst	No	No	A.3.9
\(S^*_{sen}\)	Ssen	Degree days corresponding to leaf senescence	No	No	A.3.9
\(Ph_{sen}\)	Phsen	Photoperiod corresponding to start counting senescence degree-days	No	No	A.3.9
\(T_{sen}\)	Tbsen	Base temperature for the calculation of degree days to leaf senescence	No	No	A.3.9
\(x_{sen}\)	xsen	Discrete values, to allow for any absent/proportional/more than proportional effects of temperature on senescence	No	No	A.3.9
\(y_{sen}\)	ysen	Discrete values, to allow for any absent/proportional/more than proportional effects of photoperiod on senescence	No	No	A.3.9

Plant anatomy

Symbol	R	Description	Strict	Scaled	Imputable
\(1/H_{v}\)	Al2As	Ratio of leaf area to sapwood area	No	No	A.3.7
\(RLR\)	Ar2Al	Fine root area to leaf area ratio	No	No	A.3.8
\(LW\)	LeafWidth	Leaf width	No	No	A.3.4
\(SLA\)	SLA	Specific leaf area	No	No	A.3.4
\(\rho_{leaf}\)	LeafDensity	Leaf tissue density	No	No	A.3.5
\(\rho_{wood}\)	WoodDensity	Wood tissue density	No	No	A.3.5
\(\rho_{fineroot}\)	FineRootDensity	Fine root tissue density	No	No	A.3.5
\(f_{conduits}\)	conduit2sapwood	Proportion of sapwood corresponding to xylem conduits	No	No	A.3.7
\(SRL\)	SRL	Specific fine root length	No	No	A.3.6
\(RLD\)	RLD	Fine root length density	No	No	A.3.6
\(r_{6.35}\)	r635	Ratio between the weight of leaves plus branches and the weight of leaves alone for branches of 6.35 mm	No	No	A.3.4

Radiation balance and water interception

Symbol	R	Description	Strict	Scaled	Imputable
\(k_{b}\)	kDIR	Direct light extinction coefficient	No	No	A.3.11
\(k_{PAR}\)	kPAR	PAR extinction coefficient	No	No	A.3.11
\(\alpha_{SWR}\)	alphaSWR	Short-wave radiation leaf absorbance coefficient	No	No	A.3.11
\(\gamma_{SWR}\)	gammaSWR	Short-wave radiation leaf reflectance (albedo)	No	No	A.3.11
\(s_{water}\)	g	Crown water storage capacity	No	No	A.3.11

Hydraulics, transpiration, photosynthesis

Symbol	R	Description	Strict	Scaled	Imputable
\(T_{max, LAI}\)	Tmax_LAI	Empirical coefficient relating LAI with the ratio of maximum transpiration over potential evapotranspiration	No	No	A.3.10
\(T_{max, sqLAI}\)	Tmax_LAIsq	Empirical coefficient relating squared LAI with the ratio of maximum transpiration over potential evapotranspiration	No	No	A.3.10
\(WUE_{\max}\)	WUE	Water use efficiency at VPD = 1kPa and without light or CO2 limitations	No	No	A.3.10
\(WUE_{PAR}\)	WUE_par	Coefficient describing the progressive decay of WUE with lower light levels	No	No	A.3.10
\(WUE_{CO2}\)	WUE_co2	Coefficient for WUE dependency on atmospheric CO2 concentration	No	No	A.3.10
\(WUE_{VPD}\)	WUE_vpd	Coefficient for WUE dependency on vapor pressure deficit	No	No	A.3.10
\(\Psi_{extract}\)	Psi_Extract	The water potential at which plant transpiration is 50% of its maximum	No	No	A.3.10
\(\Psi_{critic}\)	Psi_Critic	The water potential corresponding to 50% of stem xylem cavitation	No	No	A.3.16
\(g_{swmin}\)	Gwmin	Minimum stomatal conductance to water vapour	No	No	A.3.12
\(g_{swmax}\)	Gwmax	Maximum stomatal conductance to water vapour	No	No	A.3.12
\(J_{max, 298}\)	Jmax298	Maximum rate of electron transport at 298K	No	No	A.3.17
\(V_{max, 298}\)	Vmax298	Rubisco’s maximum carboxylation rate at 298K	No	No	A.3.17
\(K_{stem,max,ref}\)	Kmax_stemxylem	Maximum stem sapwood reference conductivity per leaf area unit	No	No	A.3.14
\(K_{root,max,ref}\)	Kmax_rootxylem	Maximum root sapwood reference conductivity per leaf area unit	No	No	A.3.14
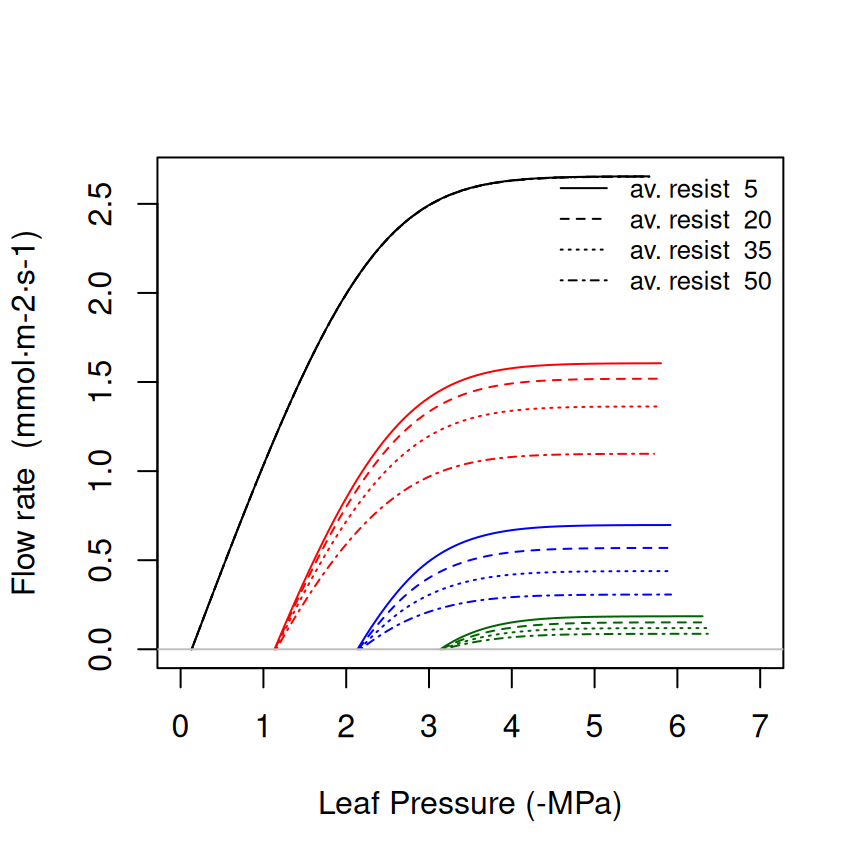
\(k_{leaf, \max}\)	VCleaf_kmax	Maximum leaf hydraulic conductance	No	A.4.2	A.3.15
\(k_{stem, \max}\)	VCstem_kmax	Maximum stem hydraulic conductance	No	A.4.1	No
\(k_{root, \max,s}\)	VCroot_kmax	Maximum root hydraulic conductance for each soil layer	No	A.4.3	No
\(k_{rhizo,\max, s}\)	VGrhizo_kmax	Maximum hydraulic conductance of the rhizosphere for each soil layer	No	A.4.4	No
\(c_{leaf}\), \(d_{leaf}\)	VCleaf_c, VCleaf_d	Parameters of the vulnerability curve for leaves	No	No	A.3.16
\(c_{stem}\), \(d_{stem}\)	VCstem_c, VCstem_d	Parameters of the vulnerability curve for stem xylem	No	No	A.3.16
\(c_{root}\), \(d_{root}\)	VCroot_c, VCroot_d	Parameters of the vulnerability curve for root xylem	No	No	A.3.16

Plant water storage

Symbol	R	Description	Strict	Scaled	Imputable
\(\epsilon_{leaf}\)	LeafEPS	Modulus of elasticity of leaves	No	No	A.3.13
\(\epsilon_{stem}\)	StemEPS	Modulus of elasticity of symplastic xylem tissue	No	No	A.3.13
\(\pi_{0,leaf}\)	LeafPI0	Osmotic potential at full turgor of leaves	No	No	A.3.13
\(\pi_{0,stem}\)	StemPI0	Osmotic potential at full turgor of symplastic xylem tissue	No	No	A.3.13
\(f_{apo,leaf}\)	LeafAF	Apoplastic fraction in leaf tissues	No	No	A.3.13
\(f_{apo,stem}\)	StemAF	Apoplastic fraction in stem tissues	No	No	A.3.13
\(V_{leaf}\)	Vleaf	Leaf water capacity per leaf area unit	No	A.4.5	No
\(V_{sapwood}\)	Vsapwood	Sapwood water capacity per leaf area unit	No	A.4.5	No

Growth and mortality

Symbol	R	Description	Strict	Scaled	Imputable
\(N_{leaf}\)	Nleaf	Leaf nitrogen concentration per dry mass	No	No	A.3.18
\(N_{sapwood}\)	Nsapwood	Sapwood nitrogen concentration per dry mass	No	No	A.3.18
\(N_{fineroot}\)	Nfineroot	Fine root nitrogen concentration per dry mass	No	No	A.3.18
\(MR_{leaf}\)	RERleaf	Leaf respiration rate at 20 ºC	No	No	A.3.18
\(MR_{sapwood}\)	RERsapwood	Living sapwood (parenchymatic tissue) respiration rate at 20 ºC	No	No	A.3.18
\(MR_{fineroot}\)	RERfineroot	Fine root respiration rate at 20 ºC	No	No	A.3.18
\(RGR_{leaf, max}\)	RGRleafmax	Maximum leaf area daily growth rate, relative to sapwood area	No	No	A.3.19
\(RGR_{cambium, max}\)	RGRsapwoodmax	Maximum tree daily sapwood growth rate relative to cambium perimeter length	No	No	A.3.19
\(RGR_{sapwood, max}\)	RGRsapwoodmax	Maximum shrub daily sapwood growth rate relative to sapwood area	No	No	A.3.19
\(RGR_{fineroot, max}\)	RGRfinerootmax	Maximum daily fine root relative growth rate	No	No	A.3.19
\(SR_{sapwood}\)	SRsapwood	Daily sapwood senescence rate	No	No	A.3.20
\(SR_{fineroot}\)	SRfineroot	Daily fine root senescence rate	No	No	A.3.20
\(RSSG\)	RSSG	Minimum relative starch for sapwood growth	No	No	A.3.21
\(C_{wood}\)	WoodC	Wood carbon content per dry weight	No	No	A.3.22
\(P_{mort,base}\)	MortalityBaselineRate	Default deterministic proportion or probability specifying the baseline reduction of cohort’s density occurring in a year	No	No	A.3.23

Recruitment

Symbol	R	Description	Strict	Scaled	Imputable
\(H_{seed}\)	SeedProductionHeight	Minimum height for seed production	No	No	A.3.24
\(TCM_{recr}\)	MinTempRecr	Minimum average temperature (Celsius) of the coldest month for successful recruitment	No	No	A.3.24
\(MI_{recr}\)	MinMoistureRecr	Minimum value of the moisture index for successful recruitment	No	No	A.3.24
\(FPAR_{recr}\)	MinFPARRecr	Minimum percentage of PAR at the ground level for successful recruitment	No	No	A.3.24
\(DBH_{recr}\)	RecrTreeDBH	Recruitment DBH for trees	No	No	A.3.24
\(H_{tree, recr}\)	RecrTreeHeight	Recruitment height for trees	No	No	A.3.24
\(N_{tree, recr}\)	RecrTreeDensity	Recruitment density for trees	No	No	A.3.24
\(Cover_{shrub, recr}\)	RecrShrubCover	Recruitment cover for shrubs	No	No	A.3.24
\(H_{shrub, recr}\)	RecrShrubHeight	Recruitment height for shrubs	No	No	A.3.24
\(Z50_{recr}\)	RecrZ50	Soil depth corresponding to 50% of fine roots for recruitment	No	No	A.3.24
\(Z95_{recr}\)	RecrZ95	Soil depth corresponding to 95% of fine roots for recruitment	No	No	A.3.24

Flammability

Symbol	R	Description	Strict	Scaled	Imputable
\(\rho_{p}\)	PD	Density of fuel particles	No	No	A.3.25
\(\sigma\)	SAV	Surface-area-to-volume ratio of the small fuel (1h) fraction (leaves and branches < 6.35mm)	No	No	A.3.25
\(h\)	HeatContent	High fuel heat content.	No	No	A.3.25
\(LI\)	PercentLignin	Percentage of lignin in leaves	No	No	A.3.25

A.3 Imputation of missing values

The following figure summarizes the percentage of missing values in SpParamsMED for different model parameters and the other model parameters used for the imputation of missing values:

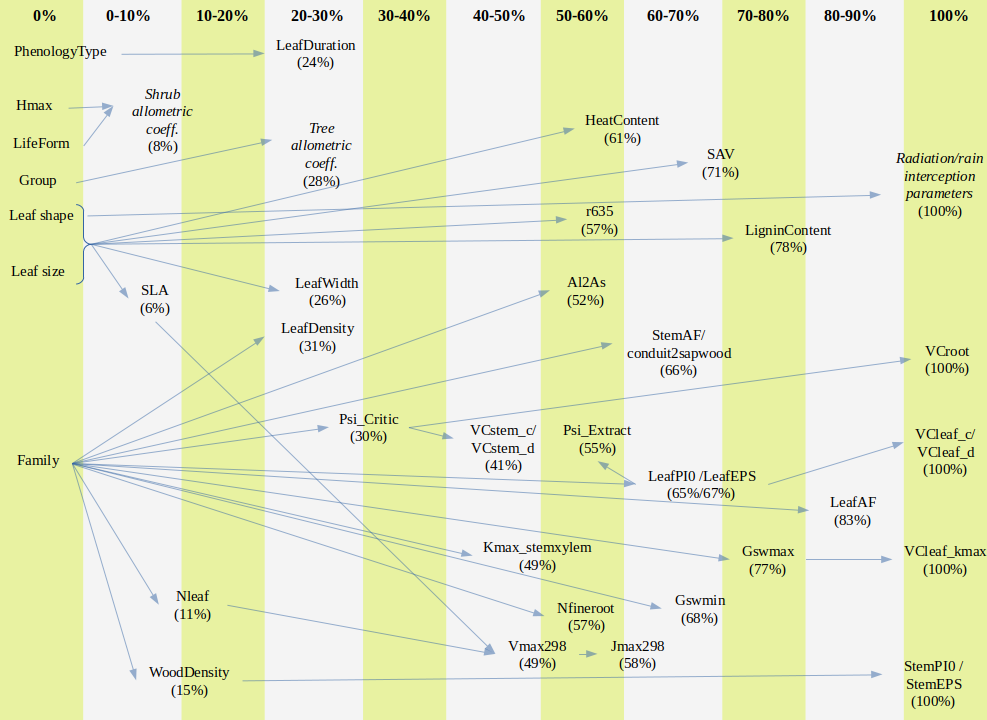
Figure A.1: Representation of imputation relationships between model parameters. The percentage of missing parameter values increases from left to right. Left-most parameters are strict.

A.3.1 Rooting depth

Parameter \(Z_{95}\) is a strict parameter, but \(Z_{50}\) can be imputated when missing, using the following formula: \[\begin{equation} Z_{50} = \exp(\log(Z_{95})/1.4) \end{equation}\]

A.3.2 Shrub allometric coefficients

Missing shrub allometric coefficients are filled using information from Raunkiaer’s life form and maximum plant height (\(H_{max}\)).

Life form	\(H_{max}\)	\(a_{ash}\)	\(b_{ash}\)	\(a_{bsh}\)	\(b_{bsh}\)	\(cr\)
Chamaephyte	[any]	24.5888	1.1662	0.7963	0.3762	0.8076
Phanerophyte	< 300 cm	1.0083	1.8700	0.7900	0.6942	0.6630
Phanerophyte	> 300 cm	5.8458	1.4944	0.3596	0.7138	0.7190
(Hemi)cryptophyte	[any]	24.5888	1.1662	0.7963	0.3762	0.9500

Allometric coefficients were taken from De Cáceres et al. (2019).

A.3.3 Tree allometric coefficients

Missing tree allometric coefficients are replaced with values depending on whether the plant species is a gymnosperm or an angiosperm:

Parameter	Gymnosperm	Angiosperm
\(a_{fbt}\)	0.1300	0.0527
\(b_{fbt}\)	1.2285	1.5782
\(c_{fbt}\)	-0.0147	-0.0066
\(a_{cw}\)	0.747	0.839
\(b_{cw}\)	0.672	0.735
\(a_{cr}\)	1.995	1.506
\(b_{1cr}\)	-0.649	-0.706
\(b_{2cr}\)	-0.020	-0.078
\(b_{3cr}\)	-0.00012	0.00018
\(c_{1cr}\)	-0.004	-0.007
\(c_{2cr}\)	-0.159	0.000
\(fHD_{min}\)	80	40
\(fHD_{max}\)	120	140

A.3.4 Leaf width, specific leaf area and fine foliar ratio

Leaf width (\(LW\)), specific leaf area (\(SLA\)) and the ratio between the weight of leaves plus branches and the weight of leaves alone for branches of 6.35 mm (\(r_{6.35}\)) are key anatomical parameters. When missing from species parameter table, default estimates for these parameters are obtained from combinations of leaf shape and leaf size:

Leaf shape	Leaf size	\(SLA\)	\(LW\)	\(r_{6.35}\)
Broad	Large	16.039	6.898	2.278
Broad	Medium	11.499	3.054	2.359
Broad	Small	9.540	0.644	3.026
Linear	Large	5.522	0.639	3.261
Linear	Medium	4.144	0.639	3.261
Linear	Small	13.189	0.639	3.261
Needle	[any]	9.024	0.379	1.716
Scale	[any]	4.544	0.101	1.483

These estimates have been obtained by averaging species-level values across combinations of the categorical variables.

A.3.5 Tissue density

Default values for the dry weight density of leaves and wood (in \(g \cdot cm^{-3}\)) are determined from taxonomic family using an internal data set (medfate:::trait_family_means):

Table A.1: Default leaf density and wood density values by taxonomic family.

	LeafDensity	WoodDensity
Acanthaceae	0.2959003	0.5684693
Achariaceae	0.2552495	0.6052036
Acoraceae	0.1000000	NA
Actinidiaceae	0.4439776	0.4092320
Adoxaceae	0.3916194	0.5157416
Aextoxicaceae	NA	0.5666667
Aizoaceae	0.0824125	NA
Akaniaceae	NA	0.5547825
Alismataceae	0.1914208	NA
Altingiaceae	0.6833971	0.6010948
Amaranthaceae	0.2045831	0.6315739
Amaryllidaceae	0.1220704	NA
Amphorogynaceae	NA	0.6097400
Anacardiaceae	0.4568088	0.5685583
Anisophylleaceae	NA	0.6734780
Annonaceae	0.3757811	0.5642062
Aphloiaceae	0.4627060	0.6205200
Apiaceae	0.2874756	0.2561785
Apocynaceae	0.2981148	0.5683635
Aptandraceae	0.3318492	0.7076756
Aquifoliaceae	0.4812626	0.5579305
Araceae	0.1659746	NA
Araliaceae	0.3118821	0.4142687
Araucariaceae	0.3447902	0.4641456
Arecaceae	0.4393589	0.5913967
Aristolochiaceae	0.2681434	0.2900000
Asparagaceae	0.1425099	0.4254258
Asphodelaceae	0.5512472	0.3951990
Aspleniaceae	0.2644557	NA
Asteraceae	0.2511093	0.4822337
Asteropeiaceae	NA	0.7554862
Atherospermataceae	0.2451357	0.4767621
Athyriaceae	0.2270615	NA
Austrobaileyaceae	0.2620992	NA
Balanopaceae	NA	0.7348976
Balsaminaceae	0.3948094	NA
Begoniaceae	0.1626789	NA
Berberidaceae	0.3599453	0.7028850
Betulaceae	0.4446528	0.5381493
Bignoniaceae	0.3572590	0.6256030
Bixaceae	0.4400000	0.3546357
Blechnaceae	0.3147993	NA
Bonnetiaceae	0.2797829	0.8400000
Boraginaceae	0.2850462	0.4987559
Brassicaceae	0.2267605	0.4516377
Bromeliaceae	0.1677139	NA
Brunelliaceae	NA	0.3112500
Bruniaceae	NA	0.5636500
Burseraceae	0.4226787	0.5205008
Buxaceae	0.2706294	0.7314511
Cactaceae	0.1819372	0.6187500
Calophyllaceae	0.4065092	0.6067855
Calycanthaceae	0.3204073	0.6500550
Calyceraceae	0.1689366	NA
Campanulaceae	0.2396318	NA
Canellaceae	NA	0.6808255
Cannabaceae	0.3529720	0.5502170
Capparaceae	0.3632941	0.6338137
Caprifoliaceae	0.3282343	0.4186392
Cardiopteridaceae	0.3136349	0.6210142
Caricaceae	0.2145354	0.1925092
Caryocaraceae	0.4728080	0.6758165
Caryophyllaceae	0.2175001	0.4356813
Casuarinaceae	0.6581279	0.8237662
Celastraceae	0.4299601	0.6414639
Centroplacaceae	NA	0.6550000
Cephalotaxaceae	NA	0.5317845
Cercidiphyllaceae	0.2896931	0.4509256
Cervantesiaceae	NA	0.6151433
Chloranthaceae	0.2125841	0.3912405
Chrysobalanaceae	0.4203120	0.7862446
Cistaceae	0.3085107	0.4830942
Cleomaceae	NA	0.6126000
Clethraceae	0.5042730	0.5336779
Clusiaceae	0.3408792	0.6987069
Cochlospermaceae	0.4378883	0.2521050
Comandraceae	0.2630059	NA
Combretaceae	0.3763244	0.6564542
Commelinaceae	0.1837240	NA
Connaraceae	0.3994071	0.5589860
Convolvulaceae	0.2614034	0.5267363
Cordiaceae	0.3528759	0.5565679
Cornaceae	0.3834263	0.6195792
Corynocarpaceae	0.2498751	0.6665337
Coulaceae	0.4529368	0.8115261
Crypteroniaceae	NA	0.4976753
Ctenolophonaceae	NA	0.7691998
Cucurbitaceae	0.2327745	0.3557651
Cunoniaceae	0.3642028	0.5754400
Cupressaceae	0.3130010	0.4938816
Curtisiaceae	NA	0.7302190
Cyatheaceae	0.1297339	0.7355404
Cycadaceae	0.6448750	NA
Cyperaceae	0.3216514	0.2346031
Cyrillaceae	NA	0.5998411
Cystopteridaceae	0.2800436	NA
Daphniphyllaceae	NA	0.5062947
Degeneriaceae	NA	0.3425000
Dennstaedtiaceae	0.2658944	NA
Dichapetalaceae	0.3522732	0.6249660
Dicksoniaceae	0.4697549	NA
Didiereaceae	NA	0.3829183
Dilleniaceae	0.3224518	0.5886310
Dioscoreaceae	0.1793296	NA
Dipentodontaceae	0.2965124	NA
Dipterocarpaceae	0.4738273	0.6409882
Droseraceae	0.1342673	NA
Dryopteridaceae	0.2796327	NA
Ebenaceae	0.4250532	0.6863834
Ehretiaceae	0.3819970	0.5687138
Elaeagnaceae	0.3121046	0.5644408
Elaeocarpaceae	0.4251434	0.5453120
Ephedraceae	NA	0.7800000
Equisetaceae	0.2590369	0.2031353
Ericaceae	0.4544895	0.6055498
Erythropalaceae	0.4039757	0.7154823
Erythroxylaceae	0.3420025	0.7799333
Escalloniaceae	0.2204192	0.5585952
Eucommiaceae	NA	0.7620000
Euphorbiaceae	0.3391137	0.4889655
Euphroniaceae	NA	0.6200000
Eupomatiaceae	0.2445709	0.5779000
Eupteleaceae	NA	0.5425200
Fabaceae	0.3851583	0.6822180
Fagaceae	0.5090006	0.6683896
Fouquieriaceae	0.2453718	NA
Frankeniaceae	NA	0.5000000
Garryaceae	0.3579628	0.6870722
Gentianaceae	0.2977642	0.6877612
Geraniaceae	0.2641399	0.1644500
Gesneriaceae	0.1013848	NA
Ginkgoaceae	0.2238538	0.4618849
Gleicheniaceae	0.4916560	NA
Gnetaceae	NA	0.6100000
Goodeniaceae	0.2051090	NA
Goupiaceae	0.4660717	0.7255032
Griseliniaceae	NA	0.6035000
Grossulariaceae	0.3485915	0.5977569
Gyrostemonaceae	NA	0.3646622
Haematococcaceae	0.2933351	NA
Haloragaceae	0.1312446	NA
Hamamelidaceae	0.3884526	0.6424968
Heliotropiaceae	NA	0.5090196
Hernandiaceae	0.4152598	0.2911796
Himantandraceae	NA	0.5126388
Humiriaceae	0.4953617	0.7700458
Hydrangeaceae	0.1690825	0.8300000
Hydrocharitaceae	0.4004979	NA
Hydrophyllaceae	0.1879433	NA
Hymenophyllaceae	0.3299410	NA
Hypericaceae	0.2990752	0.5892664
Hypoxidaceae	0.1299171	NA
Icacinaceae	NA	0.6500000
Iridaceae	0.2546647	0.3087906
Irvingiaceae	NA	0.8841681
Ixerbaceae	0.4306632	NA
Ixonanthaceae	0.3649649	0.6799304
Juglandaceae	0.5200369	0.5183733
Juncaceae	0.2014423	0.2399980
Kirkiaceae	NA	0.5079900
Lacistemataceae	0.2515838	0.4832675
Lamiaceae	0.2869862	0.5072119
Lauraceae	0.4352734	0.5415881
Lecythidaceae	0.4223276	0.6769009
Lepidobotryaceae	NA	0.4836652
Liliaceae	0.1000000	NA
Linaceae	0.2893664	0.7008226
Loasaceae	0.2700000	NA
Loganiaceae	0.4213886	0.6304908
Loranthaceae	0.3770995	0.6322000
Lycopodiaceae	0.4802434	NA
Lygodiaceae	0.5066007	NA
Lythraceae	0.3848205	0.6020073
Magnoliaceae	0.3486896	0.4707890
Malpighiaceae	0.3387076	0.6262188
Malvaceae	0.3336333	0.4855630
Marcgraviaceae	0.1698113	NA
Melanthiaceae	0.1811793	NA
Melastomataceae	0.3293654	0.6442241
Meliaceae	0.3738590	0.5899613
Melianthaceae	0.2942168	0.6210538
Menispermaceae	0.2978386	0.5205924
Menyanthaceae	0.1224487	NA
Metteniusaceae	0.5448075	0.5446187
Molluginaceae	0.1400000	NA
Monimiaceae	0.2778594	0.5179823
Montiaceae	0.0859106	NA
Moraceae	0.3518887	0.5014756
Moringaceae	NA	0.2617440
Muntingiaceae	0.3376553	0.3000000
Myodocarpaceae	NA	0.6344000
Myricaceae	0.4691690	0.5578848
Myristicaceae	0.4033709	0.4976416
Myrtaceae	0.4379521	0.7656349
Namaceae	0.5166315	0.5400000
Nothofagaceae	0.3869412	0.5955200
Nyctaginaceae	0.2497878	0.5346327
Nyssaceae	0.5290780	0.4782400
Ochnaceae	0.4787112	0.7208319
Octoknemaceae	NA	0.6880101
Olacaceae	0.3487339	0.6607729
Oleaceae	0.4051166	0.6754889
Onagraceae	0.2783621	0.4502300
Onocleaceae	0.2663707	NA
Ophioglossaceae	0.2084852	NA
Opiliaceae	0.3161129	0.6480673
Orchidaceae	0.1930601	NA
Orobanchaceae	0.2426225	0.4122466
Osmundaceae	0.2679487	NA
Oxalidaceae	0.1876039	0.5741802
Paeoniaceae	0.2851982	NA
Pandaceae	NA	0.6180903
Pandanaceae	NA	0.3309000
Papaveraceae	0.3526680	NA
Paracryphiaceae	0.4686036	0.5192721
Parnassiaceae	NA	0.3211286
Passifloraceae	0.1951307	0.5966667
Paulowniaceae	NA	0.2597687
Penaeaceae	NA	0.6994190
Pennantiaceae	NA	0.4950750
Pentaphylacaceae	0.3707627	0.5633463
Penthoraceae	0.1942110	NA
Peraceae	0.3692442	0.6620175
Peridiscaceae	NA	0.6945082
Phrymaceae	0.1098008	0.6440000
Phyllanthaceae	0.2922610	0.6160133
Phyllocladaceae	0.5787037	0.5924191
Phytolaccaceae	0.2547709	0.4116385
Picramniaceae	0.4159664	0.6208382
Picrodendraceae	0.8566338	0.8414544
Pinaceae	0.3436503	0.4480469
Piperaceae	0.2438998	0.3891992
Pittosporaceae	0.3517531	0.6168509
Plantaginaceae	0.2346642	0.2571076
Platanaceae	0.4819040	0.5298601
Plumbaginaceae	0.2603992	0.2500000
Poaceae	0.3774014	0.2860215
Podocarpaceae	0.5048204	0.5063839
Polemoniaceae	0.2775675	0.3382400
Polygalaceae	0.2708272	0.6965020
Polygonaceae	0.3254643	0.5853623
Polypodiaceae	0.2460060	NA
Pontederiaceae	0.1500000	0.4876272
Portulacaceae	0.3800000	NA
Potamogetonaceae	0.1588772	NA
Primulaceae	0.3083310	0.6369957
Proteaceae	0.4633521	0.6563858
Pteleocarpaceae	NA	0.6350000
Pteridaceae	0.2198842	0.6304250
Putranjivaceae	0.3849495	0.6921646
Quiinaceae	0.4274606	0.8260544
Ranunculaceae	0.2466518	0.3342750
Resedaceae	0.1507363	NA
Rhabdodendraceae	0.2511215	0.8000000
Rhamnaceae	0.4167308	0.6552146
Rhizophoraceae	0.3339246	0.7225795
Rosaceae	0.3956651	0.6180205
Rousseaceae	NA	0.6170000
Rubiaceae	0.3151996	0.6213798
Rutaceae	0.3406166	0.6337629
Sabiaceae	0.2269258	0.4766550
Salicaceae	0.4176502	0.5537335
Salvadoraceae	NA	0.5940900
Santalaceae	0.2638240	0.7741829
Sapindaceae	0.4055140	0.6701493
Sapotaceae	0.4524219	0.6748673
Sarcolaenaceae	NA	0.8988205
Saxifragaceae	0.1446601	NA
Schisandraceae	NA	0.5792130
Schoepfiaceae	0.3474414	0.7157100
Sciadopityaceae	NA	0.6320000
Scrophulariaceae	0.3540547	0.6839313
Selaginellaceae	0.2176000	NA
Simaroubaceae	0.3298179	0.4155088
Siparunaceae	0.2955010	0.6271829
Sladeniaceae	NA	0.5700000
Smilacaceae	0.2017709	0.7343021
Solanaceae	0.2560480	0.4931198
Staphyleaceae	0.2801318	0.4132592
Stemonuraceae	0.3123012	0.5123802
Stilbaceae	0.4577089	0.6787550
Stixaceae	NA	0.8400000
Strombosiaceae	NA	0.7027465
Styracaceae	0.3357136	0.4604059
Surianaceae	0.2843963	0.9240450
Symplocaceae	0.4826660	0.5170835
Talinaceae	0.2671358	NA
Tamaricaceae	NA	0.6636284
Tapisciaceae	NA	0.3885924
Taxaceae	0.4541759	0.5533938
Tetramelaceae	NA	0.3042230
Tetrameristaceae	NA	0.6350000
Theaceae	0.4039158	0.5640233
Thymelaeaceae	0.3129399	0.5328326
Torricelliaceae	0.3383541	NA
Trigoniaceae	NA	0.6966667
Trochodendraceae	NA	0.3366510
Turneraceae	NA	0.6265213
Typhaceae	0.1688785	NA
Ulmaceae	0.4534660	0.5979531
Urticaceae	0.3193102	0.3727392
Verbenaceae	0.3037701	0.5782080
Violaceae	0.3195701	0.6266302
Vitaceae	0.2737953	0.4965250
Vochysiaceae	0.4017484	0.5536239
Winteraceae	0.3228721	0.5236569
Ximeniaceae	0.8709687	0.8323008
Zamiaceae	0.3920216	NA
Zygophyllaceae	0.4229786	0.8554052

If the family is not any of those in the table, default values are \(\rho_{leaf} = 0.7\) and \(\rho_{wood} = 0.652\). The default value for fine root density is always \(\rho_{fineroot} = 0.165\).

A.3.6 Specific root length and root length density

Default values for specific fine root length and fine root length density are \(3870\, cm \cdot g^{-1}\) and \(10\, cm \cdot cm^{-3}\), respectively. [JUSTIFICATION MISSING]

A.3.7 Huber value and ratio of conduits to sapwood

Missing values for Al2As, the inverse of the Huber value (\(1/Hv\)) are determined from taxonomic family using an internal data set (medfate:::trait_family_means):

Table A.2: Default leaf area to sapwood area (m2/m2) / Huber value (cm2/m2) and fraction of sapwood corresponding to conduits by taxonomic family.

	Al2As	Hv	conduit2sapwood
Acanthaceae	3070.43202	3.2568707	0.6300000
Adoxaceae	4889.57295	2.0451684	NA
Altingiaceae	5129.90090	1.9493554	0.8226667
Amaranthaceae	973.13500	10.2760665	NA
Amborellaceae	4255.31915	2.3500000	NA
Anacardiaceae	19581.70525	0.5106808	0.7155889
Annonaceae	10266.65654	0.9740269	0.5685000
Apiaceae	81.15013	123.2283950	NA
Apocynaceae	19766.80134	0.5058987	0.7112500
Aquifoliaceae	4886.36183	2.0465124	0.6528500
Araliaceae	3928.39877	2.5455664	0.7785000
Araucariaceae	3846.15385	2.6000000	0.9375000
Arecaceae	5492.53731	1.8206522	NA
Asteraceae	2421.76507	4.1292197	0.7219423
Atherospermataceae	2435.95630	4.1051640	0.7560000
Austrobaileyaceae	15384.61538	0.6500000	NA
Berberidaceae	570.06271	17.5419298	NA
Betulaceae	6158.73417	1.6237103	0.8444000
Bignoniaceae	12439.80827	0.8038709	0.6360476
Bixaceae	12274.01424	0.8147294	NA
Burseraceae	12218.54705	0.8184279	0.8204286
Buxaceae	NA	NA	0.8330000
Cactaceae	2554.61304	3.9144872	0.3636905
Calophyllaceae	2662.52127	3.7558385	0.7335000
Calycanthaceae	NA	NA	0.6535500
Cannabaceae	29406.04715	0.3400661	0.7598125
Capparaceae	37525.87992	0.2664828	0.7005000
Caprifoliaceae	7568.54261	1.3212583	NA
Cardiopteridaceae	NA	NA	0.6300000
Caryocaraceae	5183.13611	1.9293339	NA
Casuarinaceae	3647.15784	2.7418610	NA
Celastraceae	8199.20056	1.2196311	NA
Chrysobalanaceae	10531.83851	0.9495018	0.5876000
Cistaceae	2129.37624	4.6962109	NA
Clusiaceae	6707.44573	1.4908805	0.5005000
Cochlospermaceae	1757.46925	5.6900000	0.7070000
Combretaceae	23650.62103	0.4228219	0.6416667
Cordiaceae	10754.86431	0.9298118	0.6300000
Cornaceae	7478.58356	1.3371516	0.6740000
Coulaceae	10676.38668	0.9366465	0.6520000
Cunoniaceae	4781.22975	2.0915121	0.7110000
Cupressaceae	1793.78915	5.5747912	0.9242857
Dichapetalaceae	7505.55229	1.3323470	NA
Dilleniaceae	7707.14493	1.2974973	0.5432500
Dipterocarpaceae	NA	NA	0.7043750
Ebenaceae	5746.58263	1.7401647	0.6300000
Ehretiaceae	3401.36054	2.9400000	NA
Elaeagnaceae	NA	NA	0.5641000
Elaeocarpaceae	8949.89085	1.1173321	0.6970000
Ericaceae	2717.89086	3.6793236	0.7423400
Erythropalaceae	11359.73085	0.8803025	NA
Erythroxylaceae	16409.39633	0.6094069	NA
Escalloniaceae	NA	NA	0.5755000
Euphorbiaceae	9648.31966	1.0364499	0.6630417
Eupomatiaceae	12833.11560	0.7792340	0.6010000
Fabaceae	13004.75675	0.7689494	0.6096376
Fagaceae	5426.21990	1.8429036	0.5965700
Garryaceae	3187.80223	3.1369575	NA
Gnetaceae	10683.76068	0.9360000	NA
Goupiaceae	NA	NA	0.6360000
Grossulariaceae	5478.25000	1.8254004	NA
Hernandiaceae	NA	NA	0.6350000
Humiriaceae	6548.42050	1.5270858	0.7283333
Juglandaceae	19643.00000	0.5090872	0.7247857
Lacistemataceae	15122.28822	0.6612756	NA
Lamiaceae	6104.68000	1.6380875	0.6817381
Lauraceae	9015.94422	1.1091462	0.6868438
Lecythidaceae	9281.45093	1.0774178	0.6052857
Linaceae	8947.01119	1.1176917	0.7125000
Loranthaceae	1657.46812	6.0332985	NA
Lythraceae	8169.26722	1.2241000	0.6600000
Magnoliaceae	NA	NA	0.8122000
Malpighiaceae	8433.60354	1.1857328	NA
Malvaceae	13911.40409	0.7188347	0.5338667
Melastomataceae	9869.59558	1.0132127	NA
Meliaceae	19432.70158	0.5145965	0.6400476
Metteniusaceae	5891.68760	1.6973066	NA
Moraceae	9851.68927	1.0150543	0.5142727
Myristicaceae	7469.72436	1.3387375	0.6990000
Myrtaceae	5657.59469	1.7675356	0.6921435
Namaceae	5314.00000	1.8818216	NA
Nothofagaceae	1642.23662	6.0892565	NA
Nyctaginaceae	43532.77978	0.2297120	0.5990000
Nyssaceae	6434.40511	1.5541452	0.7885000
Ochnaceae	10152.77493	0.9849524	0.7070000
Oleaceae	6884.98407	1.4524362	0.7367889
Pandaceae	8942.22690	1.1182897	NA
Passifloraceae	NA	NA	0.3352381
Peraceae	NA	NA	0.6800000
Phrymaceae	2450.00000	4.0816327	0.5515000
Phyllanthaceae	5535.64829	1.8064731	0.6230000
Phyllocladaceae	3344.48161	2.9900000	NA
Phytolaccaceae	88495.57522	0.1130000	NA
Picramniaceae	18326.74493	0.5456506	0.6370000
Picrodendraceae	4179.29865	2.3927460	0.5635000
Pinaceae	2648.66805	3.7754825	0.9235957
Piperaceae	17361.11111	0.5760000	NA
Platanaceae	NA	NA	0.6000000
Podocarpaceae	3147.27895	3.1773478	0.9086667
Polygalaceae	14013.36411	0.7136045	NA
Polygonaceae	8927.24402	1.1201665	0.8932000
Primulaceae	4722.91675	2.1173356	0.5600000
Proteaceae	3201.08553	3.1239403	0.5774167
Putranjivaceae	12724.49969	0.7858855	NA
Ranunculaceae	23795.00000	0.4202564	0.8130000
Rhamnaceae	3931.36135	2.5436481	0.8017273
Rhizophoraceae	4314.38201	2.3178291	0.7810000
Rosaceae	7878.01050	1.2693560	0.7084800
Rubiaceae	18589.27280	0.5379447	0.6721167
Rutaceae	11439.50207	0.8741639	0.7012857
Sabiaceae	5863.83253	1.7053693	NA
Salicaceae	12890.58086	0.7757602	0.7726667
Santalaceae	2626.05148	3.8079985	0.6450000
Sapindaceae	7991.30943	1.2513594	0.7544318
Sapotaceae	7934.19459	1.2603674	0.5657500
Scrophulariaceae	1341.78411	7.4527638	NA
Simaroubaceae	10548.49222	0.9480028	0.5160000
Siparunaceae	4727.72947	2.1151802	NA
Solanaceae	34232.00295	0.2921243	0.7681667
Staphyleaceae	7311.44239	1.3677192	NA
Stemonuraceae	NA	NA	0.4470000
Styracaceae	2782.75060	3.5935667	NA
Symplocaceae	4458.13562	2.2430901	NA
Tapisciaceae	13677.69753	0.7311172	NA
Taxaceae	NA	NA	0.8600000
Theaceae	6942.20609	1.4404643	NA
Thymelaeaceae	2285.01060	4.3763473	0.8295333
Ulmaceae	18867.92453	0.5300000	0.7870000
Urticaceae	14813.36776	0.6750659	0.6653750
Verbenaceae	8196.72131	1.2200000	0.7923500
Violaceae	7385.96177	1.3539198	0.4460000
Vitaceae	1444.04332	6.9250000	0.5700000
Vochysiaceae	5382.75239	1.8577856	0.6060000
Winteraceae	2239.03703	4.4662057	NA
Ximeniaceae	NA	NA	0.8682000
Zygophyllaceae	NA	NA	0.7712000

If there is no information derived from taxonomic family for Al2As, a default value is given depending on leaf shape and leaf size:

Leaf shape	Leaf size	Al2As
Broad	Large	4768.7
Broad	Medium	2446.1
Broad	Small	2284.9
Linear	Large	2156.0
Linear	Medium	2156.0
Linear	Small	2156.0
Needle	[any]	2751.7
Scale	[any]	1696.6

Missing values for \(f_{conduits}\), the fraction of sapwood corresponding to conduits are derived from taxonomic family (see table above). If information from taxonomic family is missing, default values are \(f_{conduits} = 0.7\) (i.e. 30% of parenchyma) for angiosperms, and \(f_{conduits} = 0.925\) (i.e. 7.5% of parenchyma) for gymnosperms (Plavcová & Jansen 2015).

A.3.8 Fine root to leaf area ratio

When missing, the fine root area to leaf area ratio is given a default value of \(RLR = 1\; m^2\cdot m^{-2}\).

A.3.9 Leaf phenology

When missing, leaf duration is assigned a value of 1 year for winter-deciduous species and 2.41 years for the remaining leaf phenology types.

Default values for leaf phenological parameters are the same regardless of the leaf phenology type:

Phenology type	t0gdd	Sgdd	Tbgdd	Ssen	Phsen	Tbsen	xsen	ysen
One-flush evergreen	50	200	0	8268	12.5	28.5	2	2
Winter deciduous	50	200	0	8268	12.5	28.5	2	2
Winter semi-deciduous	50	200	0	8268	12.5	28.5	2	2
Drought deciduous	50	200	0	8268	12.5	28.5	2	2

Leaf senescence values were derived for deciduous broad-leaved forests by Delpierre et al. (2009).

A.3.10 Basic transpiration and water-use efficiency

When the basic soil water balance model is used, \(T_{max,LAI}\) and \(T_{max,sqLAI}\) are species-specific parameters that regulate the maximum transpiration of plant cohorts (see 6.1.1). When these parameters are missing from SpParams table, they are given default values \(T_{max,LAI} = 0.134\) and \(T_{max,sqLAI} = -0.006\), according to Granier et al. (1999).

When maximum water use efficiency (\(WUE_{\max}\)) is missing, it is given a value of \(WUE_{\max} = 7.55\). By default, the coefficient describing the decay of water use efficiency with lower light levels is given a default value of \(WUE_{PAR} = 0.2812\), and the coefficient regulating the relationship between gross photosynthesis and CO2 concentration is given a default \(WUE_{CO2} = 0.0028\).

When missing, the water potential corresponding to 50% of transpiration (\(\Psi_{extract}\)) is estimated by calculating the water potential corresponding to the loss leaf turgor (\(\Psi_{tlp}\)), using equation (10.4) from Bartlett et al. (2012). The parameters of the leaf pressure-volume curve needed for applying equation (10.4) may be themselves estimated (see A.3.13). Note that \(\Psi_{tlp}\) has been found to be highly correlated to \(\Psi_{gs50}\), the water potential corresponding to 50% of stomatal conductance (Bartlett et al. 2016).

A.3.11 Radiation balance and water interception

Default value for direct light extinction is \(k_b = 0.8\). Default values for diffuse radiation extinction, absorbance, reflectance and water interception parameters depend on the leaf shape:

Leaf shape	\(k_{PAR}\)	\(\alpha_{SWR}\)	\(\gamma_{SWR}\)	\(s_{water}\)
Broad	0.55	0.70	0.18	0.5
Linear	0.45	0.70	0.15	0.8
Needle/Scale	0.50	0.70	0.14	1.0

where \(k_{PAR}\) is the diffuse PAR extinction coefficient, \(\alpha_{SWR}\) is the short-wave radiation leaf absorbance coefficient, \(\gamma_{SWR}\) is the short-wave radiation leaf reflectance (albedo) and \(s_{water}\) is the crown water storage capacity per LAI unit.

A.3.12 Stomatal conductance

Default values for minimum and maximum conductance to water vapour (\(g_{swmin}\) and \(g_{swmax}\); in \(mol\, H_2O \cdot s^{-1} \cdot m^{-2}\)) were defined depending on taxonomic family, from Duursma et al. (2018) and Hoshika et al. (2018), and stored in an internal data set (medfate:::trait_family_means):

Table A.3: Default minimum and maximum conductance to water vapour by taxonomic family.

	Gswmin	Gswmax
Acanthaceae	NA	0.2500000
Altingiaceae	NA	0.5000000
Amaranthaceae	NA	0.0750000
Amaryllidaceae	0.0180400	NA
Anacardiaceae	0.0122299	0.3148333
Apiaceae	0.0015873	NA
Aquifoliaceae	0.0005740	0.2600000
Araliaceae	0.0003902	NA
Araucariaceae	0.0018786	NA
Arecaceae	0.0004500	NA
Aristolochiaceae	0.0035896	NA
Aspleniaceae	0.0082000	NA
Asteraceae	0.0105288	0.1275000
Balsaminaceae	0.0126573	NA
Berberidaceae	0.0016500	NA
Betulaceae	0.0029731	0.3965000
Boraginaceae	0.0057402	NA
Brassicaceae	0.0106600	NA
Cactaceae	0.0000243	NA
Calophyllaceae	NA	0.1350000
Cannabaceae	NA	0.3300000
Caryophyllaceae	0.0018519	NA
Cephalotaxaceae	0.0022700	NA
Cercidiphyllaceae	NA	0.4000000
Chrysobalanaceae	NA	0.1740000
Cistaceae	0.0082820	NA
Clethraceae	NA	0.2500000
Combretaceae	0.0131200	NA
Convolvulaceae	0.0041967	NA
Cordiaceae	0.0065600	NA
Cornaceae	NA	0.3000000
Crassulaceae	0.0022751	NA
Cupressaceae	0.0063192	0.0840000
Cyperaceae	0.0190600	NA
Dipterocarpaceae	NA	0.3874722
Ehretiaceae	NA	0.2900000
Elaeagnaceae	NA	0.1700000
Ericaceae	0.0041455	0.1723333
Euphorbiaceae	0.0026500	0.2616667
Fabaceae	0.0085178	0.3066667
Fagaceae	0.0060137	0.3127601
Geraniaceae	0.0043050	NA
Hamamelidaceae	NA	0.2600000
Juglandaceae	0.0039355	0.4900000
Krameriaceae	NA	0.1600000
Lamiaceae	0.0052377	0.7300000
Lauraceae	NA	0.2212500
Magnoliaceae	0.0038800	0.3075000
Malvaceae	0.0064056	0.5532500
Meliaceae	NA	0.1600000
Moraceae	0.0064020	0.3835000
Myristicaceae	NA	0.0880000
Myrtaceae	0.0078149	0.2310769
Oleaceae	0.0046740	NA
Onagraceae	0.0169506	NA
Oxalidaceae	0.0022524	NA
Paeoniaceae	0.0082000	NA
Pentaphylacaceae	NA	0.1200000
Phyllanthaceae	0.0077900	NA
Phyllocladaceae	0.0050406	NA
Pinaceae	0.0036139	0.1776737
Plantaginaceae	0.0061086	NA
Platanaceae	0.0066100	0.4250000
Poaceae	0.0160657	0.4691495
Podocarpaceae	0.0076971	NA
Polygalaceae	NA	0.0870000
Polygonaceae	0.0139237	NA
Pontederiaceae	NA	0.2400000
Proteaceae	0.0075187	NA
Ranunculaceae	0.0096204	NA
Rosaceae	0.0092820	0.5316667
Rubiaceae	0.0061500	NA
Rutaceae	0.0090200	NA
Salicaceae	0.0086680	0.3373333
Sapindaceae	0.0035583	0.2119630
Sapotaceae	NA	0.1870000
Sciadopityaceae	0.0066554	NA
Simaroubaceae	NA	0.6320000
Solanaceae	NA	0.6000000
Taxaceae	0.0037033	NA
Theaceae	0.0068781	0.4600000
Ulmaceae	NA	0.4425000
Urticaceae	NA	0.6075000
Verbenaceae	0.0120000	NA
Vitaceae	0.0056426	NA
Zygophyllaceae	NA	0.1580769

If there is no information derived from taxonomic family, \(g_{swmin} = 0.0049\) and \(g_{swmax} = 0.200\).

A.3.13 Pressure-volume curves

Parameters of the pressure-volume curve (i.e. \(\pi_{0,stem}\) and \(\epsilon_{stem}\)) for leaf and stem symplastic tissue are required for each species.

When parameters for stem tissue are missing, medfate estimates them from wood density following Christoffersen et al. (2016): \[\begin{equation} \pi_{0,stem} = 0.52 - 4.16 \cdot \rho_{wood} \end{equation}\]

\[\begin{equation} \epsilon_{stem} = \sqrt{1.02 \cdot e^{8.5\cdot \rho_{wood}}-2.89} \end{equation}\] while the apoplastic fraction of stem is assumed \(f_{apo,stem} = f_{conduits}\) (see A.3.7).

Default values for leaf pressure-volume parameters, i.e. \(\pi_{0,leaf}\), \(\epsilon_{leaf}\) and \(f_{apo,leaf}\), are determined from taxonomic family using an internal data set (medfate:::trait_family_means):

Table A.4: Default leaf pressure-volume parameters by taxonomic family.

	LeafPI0	LeafEPS	LeafAF
Acanthaceae	-3.395000	23.230000	0.1270000
Adoxaceae	-1.560000	12.790000	NA
Amaranthaceae	-2.250000	NA	NA
Anacardiaceae	-1.700000	12.760000	NA
Annonaceae	-2.160000	23.710000	NA
Apocynaceae	-2.390000	20.940000	NA
Aquifoliaceae	-2.300000	20.700000	0.4000000
Araliaceae	-1.528503	11.231462	0.4065000
Arecaceae	-3.400000	73.400000	0.2000000
Aspleniaceae	-1.240000	35.300000	NA
Asteraceae	-1.471389	14.491429	0.2435000
Atherospermataceae	-1.340000	8.380000	NA
Betulaceae	-1.246984	5.498667	NA
Bignoniaceae	-1.990000	17.610000	0.1770000
Boraginaceae	-1.140000	NA	NA
Brassicaceae	-1.485000	7.710000	0.2320000
Burseraceae	-1.435000	14.980000	NA
Cactaceae	NA	8.700000	NA
Cannabaceae	-1.580000	5.180000	NA
Capparaceae	-2.840000	14.750000	0.1723333
Caryocaraceae	-1.710000	11.340000	NA
Celastraceae	-2.600000	19.060000	NA
Combretaceae	-2.110000	6.830000	NA
Connaraceae	-2.250000	18.010000	NA
Convolvulaceae	-1.320000	NA	NA
Cordiaceae	-1.647500	11.295938	NA
Cucurbitaceae	-0.980000	NA	NA
Cupressaceae	-1.480000	12.600000	0.2720000
Dipterocarpaceae	-1.131429	23.630000	0.4634286
Dryopteridaceae	-1.425000	48.950000	NA
Ebenaceae	-2.110000	14.650000	NA
Ericaceae	-1.670000	14.382000	0.4660000
Erythroxylaceae	-1.916667	16.993333	NA
Euphorbiaceae	-1.260000	17.570000	0.4745000
Fabaceae	-1.641724	13.577917	0.2609091
Fagaceae	-1.994080	18.132800	0.2206667
Geraniaceae	-0.730000	3.740000	NA
Goodeniaceae	-1.500000	NA	NA
Grossulariaceae	-1.845000	NA	NA
Hydrophyllaceae	-1.260000	NA	NA
Irvingiaceae	-1.690000	38.380000	0.4760000
Lamiaceae	-1.184000	6.120000	0.2200000
Lauraceae	-2.074728	16.763373	0.1760000
Lindsaeaceae	-1.970000	7.340000	0.1700000
Lythraceae	-1.535000	6.055000	NA
Magnoliaceae	-1.430000	9.140000	0.1560000
Malpighiaceae	-1.540000	9.450000	NA
Malvaceae	-2.110000	17.730000	NA
Melastomataceae	-1.754000	12.306667	NA
Moraceae	-1.353563	13.575000	NA
Myrtaceae	-1.852385	14.462948	0.4006000
Nothofagaceae	-1.480000	8.380000	NA
Nyctaginaceae	-1.280000	NA	NA
Oleaceae	-2.060557	14.205556	NA
Onagraceae	-1.200000	NA	NA
Orchidaceae	-0.530000	14.766667	0.2366667
Paeoniaceae	-1.860000	NA	NA
Papaveraceae	-1.610000	NA	NA
Pentaphylacaceae	-1.550000	9.270000	NA
Phyllanthaceae	-1.263333	13.966667	0.3036667
Pinaceae	-1.771562	17.837500	0.2587500
Pittosporaceae	-1.946262	9.759533	0.3610000
Platanaceae	-1.390000	8.810000	0.3600000
Poaceae	-1.137143	4.856667	NA
Polygalaceae	-1.590000	26.760000	0.4140000
Polygonaceae	-1.600000	5.030000	NA
Polypodiaceae	-1.158333	34.250000	0.2100000
Primulaceae	-1.700000	15.320000	NA
Proteaceae	-2.114345	15.525000	NA
Rhamnaceae	-2.041667	6.200000	0.0770000
Rhizophoraceae	-2.320000	9.650000	NA
Rosaceae	-1.766687	10.812958	0.4820000
Rubiaceae	-1.681563	12.938015	0.4500000
Salicaceae	-1.891667	15.555000	NA
Sapindaceae	-1.357544	7.156992	0.1000000
Sapotaceae	-1.785000	17.835000	0.3830000
Scrophulariaceae	-1.210000	NA	NA
Simmondsiaceae	-2.420000	NA	NA
Solanaceae	-1.072000	9.465000	NA
Styracaceae	-2.280000	24.565000	NA
Symplocaceae	-1.485000	NA	NA
Tetrameristaceae	-2.970000	NA	NA
Urticaceae	-1.040250	9.126500	NA
Verbenaceae	-1.100000	4.850000	0.2270000
Violaceae	-1.390000	17.840000	0.3720000
Vitaceae	-1.292900	6.647000	NA
Vochysiaceae	-2.135000	19.995000	NA
Winteraceae	-1.480000	11.620000	NA
Zygophyllaceae	-2.780000	NA	NA

If family-level values are missing, following Bartlett et al. (2012) average values for Mediterranean climate leaves are taken as defaults, i.e. \(\pi_{0,leaf} = -2\) MPa, \(\epsilon_{leaf} = 17\), whereas a 29% leaf apoplastic fraction is assumed (i.e. \(f_{apo,leaf} = 0.29\)).

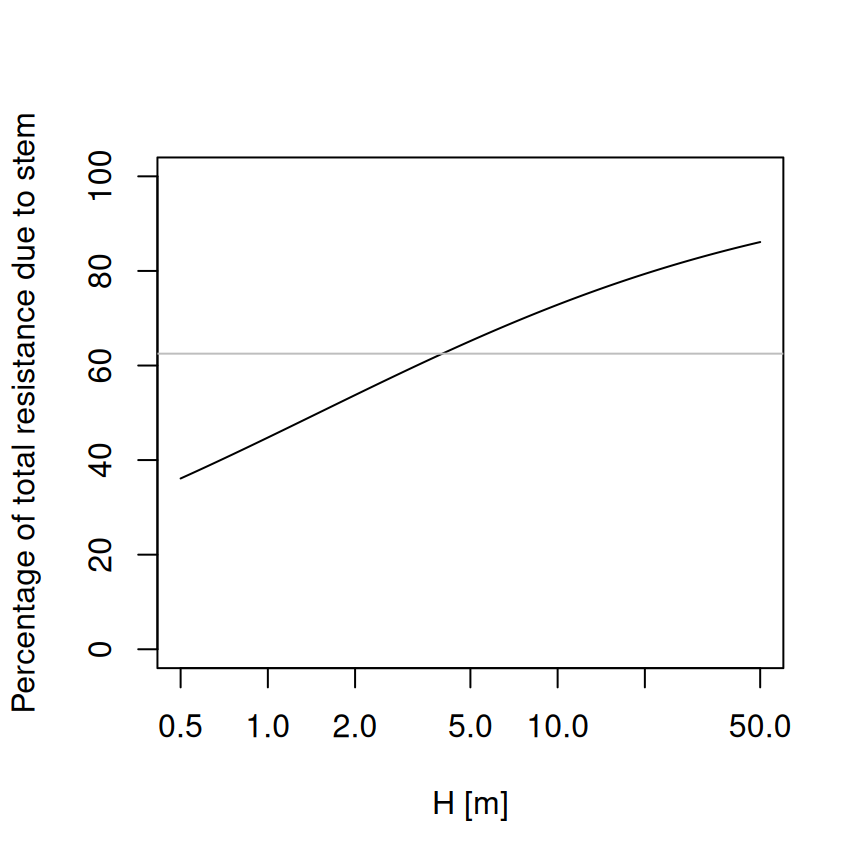
A.3.14 Stem and root maximum hydraulic conductivity

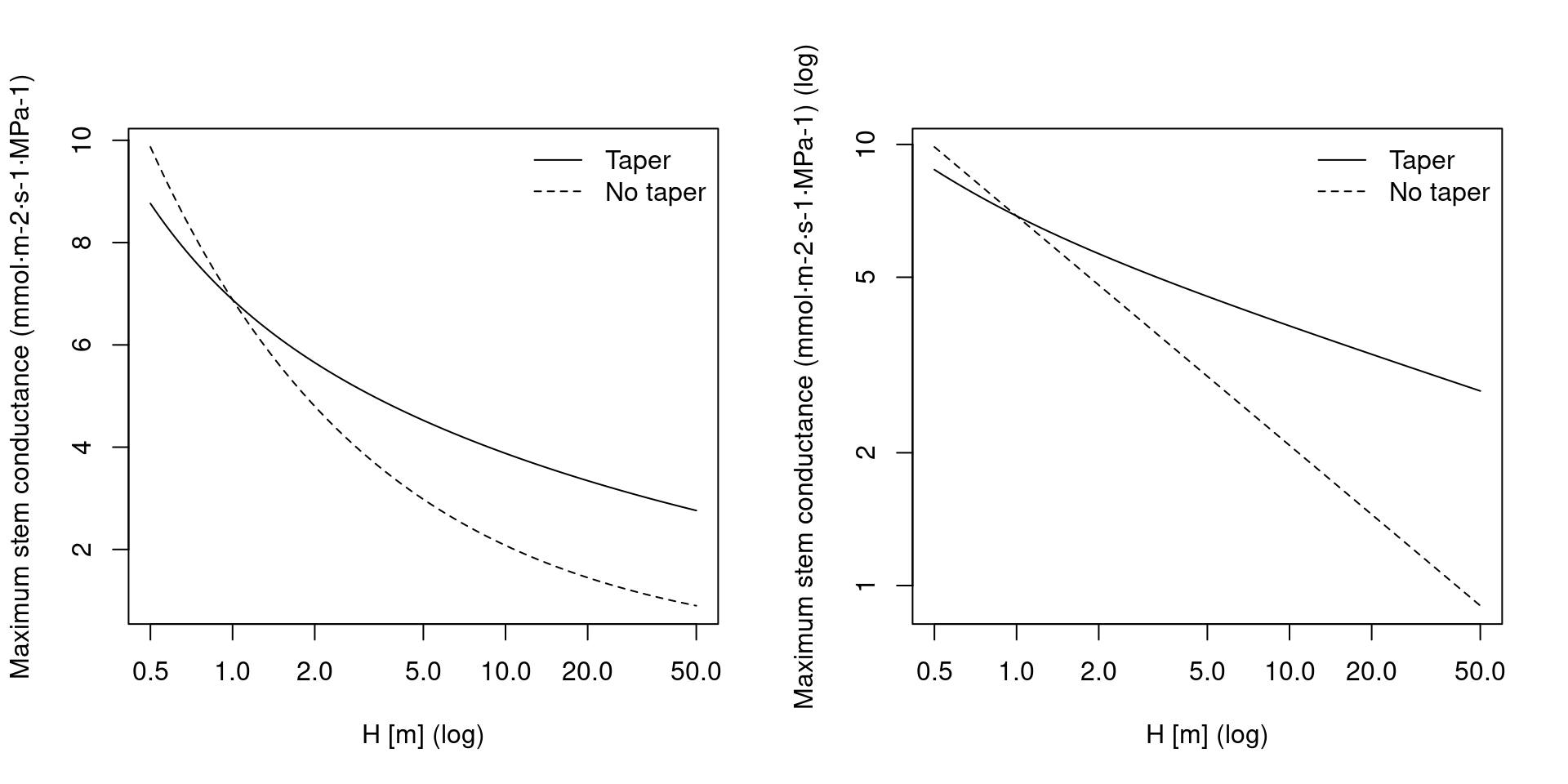
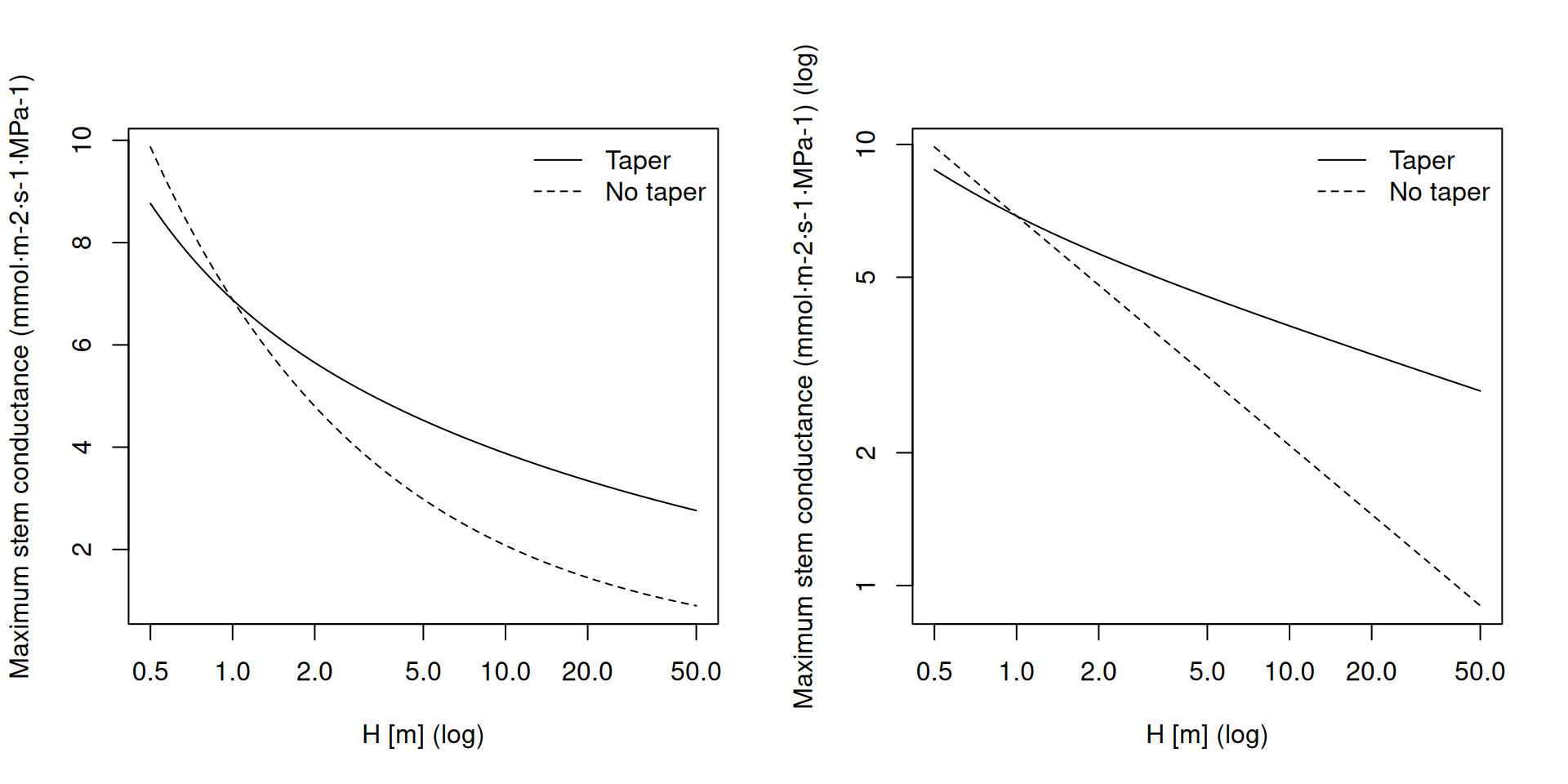
Tissue-level maximum conductivity parameters (i.e. \(K_{stem,max,ref}\) and \(K_{root,max,ref}\)) are not direct parameters to simulation functions. Instead, theay are scaled to estimate stem- and root-level hydraulic conductances (i.e. \(k_{stem, \max}\) and \(k_{root, \max}\)) using plant size (see A.4.1 and A.4.3 for details). \(K_{stem,max,ref}\) and \(K_{root,max,ref}\) are supplied via species parameter table and missing values can therefore occur.

Default values for \(K_{stem,max,ref}\) are determined from taxonomic family using an internal data set (medfate:::trait_family_means):

Table A.5: Default maximum stem hydraulic conductivity by taxonomic family.

	Kmax_stemxylem
Adoxaceae	4.0535575
Altingiaceae	0.5050000
Amaranthaceae	0.0819000
Amborellaceae	0.5400000
Anacardiaceae	4.0772016
Annonaceae	5.2706667
Apiaceae	0.5150000
Apocynaceae	2.5651667
Aquifoliaceae	0.2255757
Araliaceae	1.6809011
Araucariaceae	0.7322500
Asteraceae	0.4986571
Austrobaileyaceae	2.3000000
Berberidaceae	0.0873333
Betulaceae	2.8733374
Bignoniaceae	2.1014900
Bruniaceae	0.2515000
Burseraceae	3.4050000
Cactaceae	1.8688095
Calophyllaceae	0.8982857
Cannabaceae	4.3396105
Capparaceae	0.5572667
Caprifoliaceae	0.2521010
Caryocaraceae	1.7587273
Casuarinaceae	1.8954048
Cistaceae	0.3958482
Clusiaceae	0.5950000
Cochlospermaceae	7.7500000
Combretaceae	5.7436667
Convolvulaceae	2.2000000
Cordiaceae	4.4607389
Cornaceae	2.3439777
Cupressaceae	0.9325131
Daphniphyllaceae	0.4600000
Dennstaedtiaceae	21.9800000
Dilleniaceae	1.2500000
Dipterocarpaceae	8.8857143
Ebenaceae	1.5527759
Ehretiaceae	0.4100000
Ericaceae	0.6151806
Erythroxylaceae	0.5352000
Euphorbiaceae	3.3816717
Eupomatiaceae	1.1239700
Fabaceae	2.9075403
Fagaceae	2.5306061
Garryaceae	1.9333333
Gnetaceae	1.2900000
Iteaceae	0.4500000
Juglandaceae	4.2050000
Lamiaceae	4.8686077
Lauraceae	1.1201255
Lecythidaceae	6.5443450
Loranthaceae	0.2817696
Lythraceae	6.1800000
Malpighiaceae	11.0500000
Malvaceae	5.0140647
Melastomataceae	3.2448243
Meliaceae	3.5074214
Moraceae	4.2635627
Myricaceae	2.0300000
Myrothamnaceae	0.8700000
Myrtaceae	3.0899244
Nothofagaceae	0.7973333
Nyctaginaceae	3.4236667
Nyssaceae	0.1800000
Ochnaceae	0.9111500
Oleaceae	0.8444824
Onagraceae	1.0800000
Pandaceae	1.1963139
Phyllanthaceae	2.5362078
Phyllocladaceae	0.6930000
Phytolaccaceae	2.0410000
Picrodendraceae	3.9400000
Pinaceae	0.7547927
Piperaceae	4.4389250
Pittosporaceae	1.7800000
Poaceae	4.5583333
Podocarpaceae	0.4627272
Polygalaceae	0.1615533
Polygonaceae	2.4000000
Primulaceae	1.4938311
Proteaceae	1.6704393
Putranjivaceae	0.6000000
Rhamnaceae	1.9312597
Rhizophoraceae	1.1050000
Rosaceae	5.6895709
Rubiaceae	2.1240290
Rutaceae	1.5498517
Salicaceae	3.0508423
Santalaceae	1.8595493
Sapindaceae	2.5607242
Sapotaceae	0.5590170
Sciadopityaceae	0.4400000
Scrophulariaceae	0.2350000
Simaroubaceae	2.4300000
Solanaceae	3.6970125
Stachyuraceae	0.5500000
Staphyleaceae	2.6500000
Styracaceae	2.3407222
Symplocaceae	3.2000000
Tamaricaceae	2.6600000
Taxaceae	0.3200000
Theaceae	2.8179558
Thymelaeaceae	0.5627650
Ulmaceae	0.6210000
Urticaceae	4.9860000
Verbenaceae	1.7200000
Vochysiaceae	1.4756667
Winteraceae	0.4133333

If family-level values are missing, suitable \(K_{stem,max,ref}\) values are decided according to combinations of taxon group (either Angiosperm or Gymnosperm), growth form (either tree or shrub) and leaf phenology (Maherali et al. 2004):

Group	Growth form	Leaf phenology	\(K_{stem,max,ref}\)
Angiosperm	Tree	Winter-(semi)deciduous	1.58
Angiosperm	Shrub	Winter-(semi)deciduous	1.55
Angiosperm	Tree/Shrub	Evergreen	2.43
Gymnosperm	Tree	any	0.48
Gymnosperm	Shrub	any	0.24

Following Oliveras et al. (2003), missing values for \(K_{root,max,ref}\) are assumed to be four-times the values given or estimated for \(K_{stem,max,ref}\).

A.3.15 Leaf maximum hydraulic conductance

Leaf maximum hydraulic conductance (\(k_{l, max}\), in \(mmol \cdot m^{-2} \cdot s^{-1} \cdot MPa^{-1}\)) is an input parameter that should be provided for each species. When missing, leaf maximum hydraulic conductance can be estimated from maximum stomatal conductance (\(g_{swmax}\)), following Franks (2006) (original coefficients were modified for better fit): \[\begin{equation} k_{l, max} = (g_{swmax}/0.015)^{1/1.3} \end{equation}\] Note that values for \(g_{swmax}\) may also be imputed (see A.3.12).

A.3.16 Xylem vulnerability

Default values for \(\Psi_{50,stem}\) are determined from taxonomic family using an internal data set (medfate:::trait_family_means):

Table A.6: Default stem P50 values by taxonomic family.

	P50
Adoxaceae	-3.0384833
Altingiaceae	-2.0370147
Amaranthaceae	-2.4252402
Amborellaceae	-3.0000000
Anacardiaceae	-2.6535235
Annonaceae	-2.5276068
Apiaceae	-5.7000000
Apocynaceae	-2.4864334
Aquifoliaceae	-3.6437782
Araliaceae	-1.6530859
Araucariaceae	-2.6183226
Arecaceae	-1.8100000
Asparagaceae	-1.6960000
Asteraceae	-3.2565860
Atherospermataceae	-3.0063333
Austrobaileyaceae	-0.4990000
Berberidaceae	-4.5000000
Betulaceae	-2.1017591
Bignoniaceae	-0.8616667
Boraginaceae	-3.5677066
Bruniaceae	-3.3883558
Burseraceae	-1.3054970
Buxaceae	-8.0000000
Cactaceae	-1.2875000
Calophyllaceae	-1.5400000
Calycanthaceae	-1.2808475
Canellaceae	-0.2320000
Cannabaceae	-1.5325304
Capparaceae	-2.3615234
Caprifoliaceae	-5.5144833
Caryocaraceae	-1.6766667
Casuarinaceae	-2.1750000
Celastraceae	-3.4679167
Chloranthaceae	-1.7228571
Chrysobalanaceae	-2.2000000
Cistaceae	-7.1951892
Cleomaceae	-2.1842678
Clusiaceae	-1.3172327
Cochlospermaceae	-1.4400000
Combretaceae	-1.8483333
Convolvulaceae	-1.5987102
Cordiaceae	-2.3307795
Cornaceae	-4.1378833
Cunoniaceae	-1.1500000
Cupressaceae	-8.3049767
Daphniphyllaceae	-0.5985705
Dennstaedtiaceae	-1.9900000
Dilleniaceae	-1.4112676
Dipterocarpaceae	-0.3628571
Dryopteridaceae	-2.5797602
Ebenaceae	-1.5093287
Ehretiaceae	-3.8200000
Ericaceae	-2.8142685
Euphorbiaceae	-1.4638127
Eupomatiaceae	-0.3950000
Fabaceae	-2.3909838
Fagaceae	-2.5878534
Fouquieriaceae	-1.3452785
Garryaceae	-6.2691850
Ginkgoaceae	-4.3306349
Gnetaceae	-3.8601667
Grossulariaceae	-3.5658333
Haematococcaceae	-1.0161048
Himantandraceae	-1.3000000
Iteaceae	-2.4945237
Juglandaceae	-1.5701852
Lamiaceae	-4.1494102
Lauraceae	-2.1528796
Lecythidaceae	-1.3583333
Lomariopsidaceae	-1.1192688
Lythraceae	-1.1835117
Magnoliaceae	-1.6162070
Malpighiaceae	-1.2600000
Malvaceae	-1.5443759
Melastomataceae	-2.2465000
Meliaceae	-1.6824730
Menispermaceae	-0.6400000
Moraceae	-1.0012407
Myricaceae	-1.6301207
Myrtaceae	-2.1681342
Nothofagaceae	-2.5384687
Nyctaginaceae	-3.3618225
Nyssaceae	-1.7354355
Ochnaceae	-1.6475300
Oleaceae	-3.3224338
Onagraceae	-1.6250000
Pandaceae	-2.6000000
Pentaphylacaceae	-1.2000000
Phyllanthaceae	-1.9312493
Phyllocladaceae	-6.9215266
Phytolaccaceae	-2.9000000
Pinaceae	-3.9399344
Pittosporaceae	-1.9328674
Platanaceae	-1.5447656
Poaceae	-2.5980959
Podocarpaceae	-3.6786525
Polygalaceae	-1.5000000
Polygonaceae	-1.8324549
Polypodiaceae	-1.4328381
Primulaceae	-2.4159524
Proteaceae	-3.0023208
Pteridaceae	-1.6296520
Putranjivaceae	-2.2150279
Ranunculaceae	-1.6100000
Rhamnaceae	-5.0583305
Rhizophoraceae	-5.1853958
Rosaceae	-4.2920879
Rubiaceae	-2.7428916
Rutaceae	-1.4957143
Salicaceae	-1.9309521
Sapindaceae	-2.3003821
Sapotaceae	-1.9824490
Sarcobataceae	-2.1745285
Schisandraceae	-2.6653333
Sciadopityaceae	-2.4279818
Simaroubaceae	-1.5043567
Solanaceae	-1.6191103
Stachyuraceae	-4.0791455
Staphyleaceae	-1.9981312
Stemonuraceae	-0.1800000
Styracaceae	-2.6750000
Symplocaceae	-2.1074074
Tamaricaceae	-1.2780403
Taxaceae	-6.9838493
Tectariaceae	-1.2443660
Theaceae	-3.3275000
Thelypteridaceae	-1.1367341
Thymelaeaceae	-4.3968716
Trimeniaceae	-0.8180000
Trochodendraceae	-1.8850000
Urticaceae	-0.7786495
Verbenaceae	-1.7193146
Violaceae	-2.5751935
Vitaceae	-0.3520000
Vochysiaceae	-1.4583013
Winteraceae	-3.4099667
Zygophyllaceae	-3.8233368

If family-level values is missing, a suitable estimate of \(\Psi_{50,stem}\) the water potential corresponding to 50% of conductance loss, can be obtained from Maherali et al. (2004) according to combinations of taxon group (either Angiosperm or Gymnosperm), growth form (either tree or shrub) and leaf phenology:

Group	Growth form	Leaf phenology	\(\Psi_{50,stem}\)
Angiosperm	Tree/Shrub	Winter-(semi)deciduous	-2.34
Angiosperm	Tree	Evergreen	-1.51
Angiosperm	Shrub	Evergreen	-5.09
Gymnosperm	Tree	any	-4.17
Gymnosperm	Shrub	any	-8.95

\(\Psi_{50,stem}\) estimates are taken for parameter \(\Psi_{critic}\), in the case of the basic water balance model.

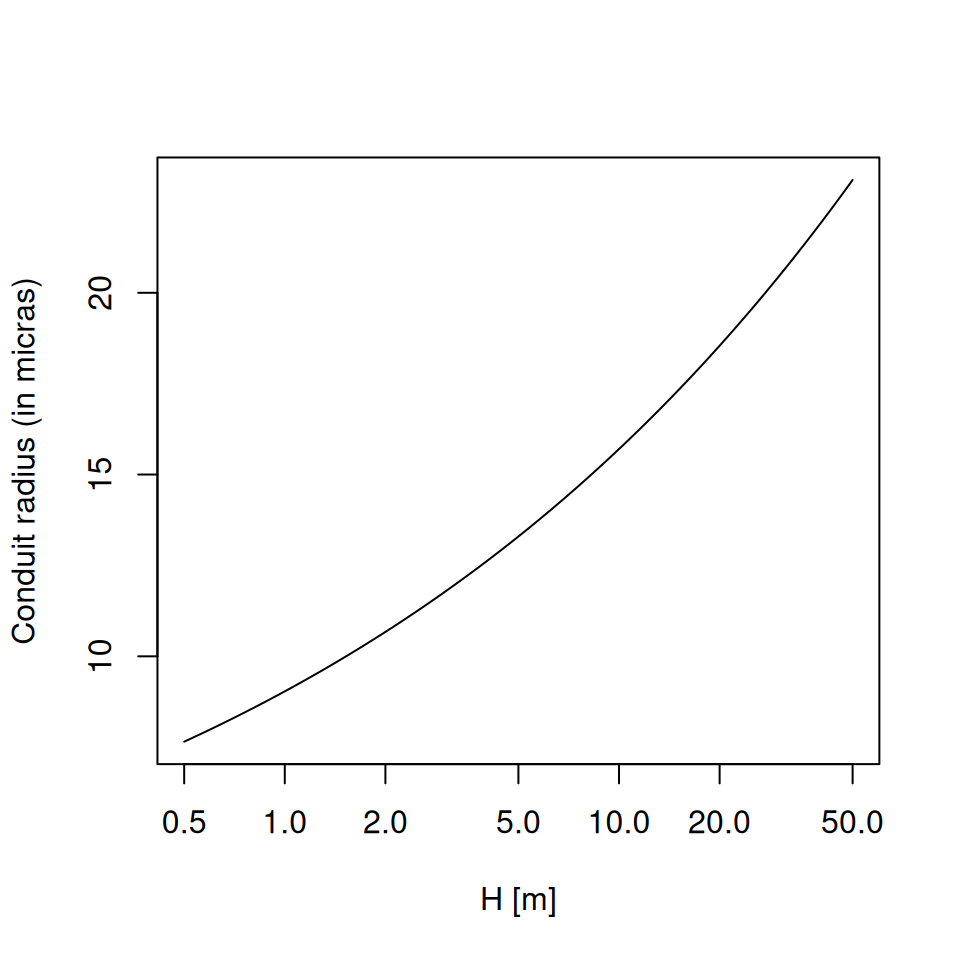
Vulnerability curves in the advanced model need to be specified for leaves, stem and root segments via the two parameters of the Weibull function (see 10.2). When any of the parameters of the stem vulnerability curve is missing, a regression equation using data from Choat et al. (2012) can be used to estimate \(\Psi_{88,stem}\) from \(\Psi_{50,stem}\): \[\begin{equation} \Psi_{88,stem} = -1.4264 + 1.2593 \cdot \Psi_{50,stem} \end{equation}\]

Finally, estimates for \(c_{stem}\) and \(d_{stem}\) are obtained from \(\Psi_{50,stem}\) and \(\Psi_{88,stem}\) via function hydraulics_psi2Weibull().

Vulnerability curves for root xylem are less common than for stem xylem. If these values are missing, \(\Psi_{50,stem}\) is first estimated according to its definition and the stem vulnerability curve parameters, \(c_{stem}\) and \(d_{stem}\). Then, a relationship from Bartlett et al. (2016) is used to estimate \(\Psi_{50, root}\) from \(\Psi_{50,stem}\): \[\begin{equation} \Psi_{50, root} = 0.4892 + 0.742 \cdot \Psi_{50,stem} \end{equation}\] Finally, \(\Psi_{88,stem}\) and the Weibull vulnerability parameters are obtained as explained for stems.

Vulnerability curves for leaf xylem are also less common than for stem xylem. If these values are missing, the water potential at turgor los point \(\Psi_{tlp}\) is first estimated from \(\pi_{leaf}\) and \(\epsilon_{leaf}\) according to eq. (10.4). Then, a relationship calibrated with data from Bartlett et al. (2016) is used to estimate \(\Psi_{50, leaf}\) from \(\Psi_{tlp}\): \[\begin{equation} \Psi_{50, leaf} = 0.2486 + 0.9944 \cdot \Psi_{tlp} \end{equation}\] Finally, \(\Psi_{88,leaf}\) and the Weibull vulnerability parameters are obtained as explained for stems.

A.3.17 Photosynthesis rates

Rubisco’s maximum carboxylation rate at 25ºC (\(V_{max, 298}\), in \(\mu mol CO_2 \cdot s^{-1} \cdot m^{-2}\)) is a required input parameter for each species (Vmax298). When missing, the work by Walker et al. (2014) suggests that suitable estimates can be derived from \(SLA\) and \(N_{area}\), the latter being the nitrogen concentration per leaf area: \[\begin{equation} V_{max, 298} = e^{1.993 + 2.555\cdot \log(N_{area}) - 0.372 \cdot \log(SLA) + 0.422 \cdot \log(N_{area})\cdot \log(SLA) } \end{equation}\]

In turn, imputation for \(SLA\) is explained in A.3.4, whereas values for \(N_{area}\) are determined from \(N_{leaf}\) and \(SLA\), being \(N_{leaf}\) estimated as indicated in A.3.18. Would \(N_{leaf}\) and \(SLA\) values be both unavailable, a default value of 100 \(\mu mol CO_2 \cdot s^{-1} \cdot m^{-2}\) is used for \(V_{max, 298}\) imputation.

When the maximum rate of electron transport at the same temperature (\(J_{max, 298}\)) is not provided by the user, it can be estimated from \(V_{max, 298}\) using (Walker et al. 2014):

\[\begin{equation} J_{max, 298} = e^{1.197 + 0.847\cdot \log(V_{max,298})} \end{equation}\]

A.3.18 Maintenance respiration rates

When missing at the species parameter table, maintenance respiration rates for leaves, sapwood and fine roots (\(RER_{leaf}\), \(RER_{sapwood}\) and \(RER_{fineroot}\); all in \(g\,gluc\cdot g\,dry^{-1}\cdot day^{-1}\)) are estimated from corresponding tissue nitrogen concentrations (\(N_{leaf}\), \(N_{sapwood}\) and \(N_{fineroot}\); all in \(mg\,N \cdot g\,dry^{-1}\)) following the equations given by Reich et al. (2008) (after appropriate unit conversion): \[\begin{eqnarray} RER_{leaf} &=& e^{0.691+ 1.639 \cdot \log(N_{leaf}))} \\ RER_{sapwood} &=& e^{1.024 + 1.344 \cdot \log(N_{sapwood}))} \\ RER_{fineroot} &=& e^{0.980 + 1.352 \cdot \log(N_{fineroot}))} \end{eqnarray}\] where in the previous equations nitrogen concentrations are in \(mmol\,N\cdot g\,dry^{-1}\) and respiration rates in \(nmol\,CO2\cdot g\,dry^{-1}\cdot s^{-1}\).

In turn, when tissue nitrogen concentrations are missing they are estimated from taxonomic family using an internal data set (medfate:::trait_family_means):

Table A.7: Default nitrogen concentration per dry mass in different tissues by taxonomic family.

	Nleaf	Nsapwood	Nfineroot
Acanthaceae	27.122403	NA	5.580000
Achariaceae	22.162815	NA	NA
Acoraceae	18.000000	NA	NA
Actinidiaceae	20.183321	NA	NA
Adoxaceae	20.566364	NA	11.013750
Aextoxicaceae	9.621429	NA	NA
Aizoaceae	14.800000	NA	NA
Alismataceae	27.287834	NA	NA
Alstroemeriaceae	19.402857	NA	NA
Altingiaceae	15.462547	NA	7.550000
Amaranthaceae	23.740694	NA	12.411441
Amaryllidaceae	28.734076	NA	11.440000
Amphorogynaceae	25.236766	NA	NA
Anacardiaceae	17.914439	NA	10.539737
Annonaceae	23.593695	NA	23.830391
Apiaceae	24.746891	NA	10.787434
Apocynaceae	21.754119	NA	16.845575
Aptandraceae	28.435524	NA	NA
Aquifoliaceae	14.645818	NA	14.324450
Araceae	22.255347	NA	NA
Araliaceae	18.093569	NA	20.500000
Araucariaceae	12.622035	NA	13.000000
Arecaceae	18.349681	NA	13.216667
Aristolochiaceae	31.726525	NA	NA
Asparagaceae	22.875870	NA	NA
Asphodelaceae	12.352222	NA	NA
Aspleniaceae	28.260000	NA	NA
Asteraceae	22.036543	NA	9.346061
Atherospermataceae	17.869722	NA	23.200000
Athyriaceae	26.901037	NA	NA
Aulacomniaceae	8.000000	NA	NA
Balsaminaceae	36.003950	NA	NA
Begoniaceae	34.200000	NA	NA
Berberidaceae	17.997372	NA	21.087500
Betulaceae	24.194029	14.505149	13.430951
Bignoniaceae	23.830902	6.575973	19.915047
Bixaceae	25.531043	NA	NA
Blechnaceae	11.749050	NA	NA
Bonnetiaceae	9.800000	NA	NA
Boraginaceae	23.032555	NA	NA
Brassicaceae	34.316821	NA	18.501306
Bromeliaceae	9.559591	NA	NA
Brunelliaceae	21.006960	NA	NA
Bruniaceae	7.781667	NA	NA
Burseraceae	19.028712	NA	10.964427
Butomaceae	42.600000	NA	NA
Buxaceae	22.691830	NA	NA
Cabombaceae	19.500000	NA	NA
Cactaceae	16.988641	NA	NA
Calophyllaceae	12.424790	NA	NA
Calycanthaceae	17.400000	NA	NA
Calyceraceae	43.000000	NA	NA
Campanulaceae	27.682767	NA	5.721013
Cannabaceae	28.941055	NA	NA
Cannaceae	39.700000	NA	NA
Capparaceae	30.523096	9.456375	NA
Caprifoliaceae	19.333331	NA	12.382333
Cardiopteridaceae	19.882555	NA	NA
Caricaceae	36.177864	NA	NA
Caryocaraceae	18.085982	NA	NA
Caryophyllaceae	22.682234	NA	12.024146
Casuarinaceae	13.167778	NA	NA
Celastraceae	18.486005	NA	16.244311
Centroplacaceae	15.890000	NA	NA
Cephalotaxaceae	19.300000	NA	NA
Chloranthaceae	18.710157	NA	NA
Chrysobalanaceae	16.190293	NA	NA
Cibotiaceae	17.187976	NA	NA
Cistaceae	17.353120	NA	10.170000
Cleomaceae	40.580000	NA	NA
Clethraceae	14.113977	NA	NA
Clusiaceae	15.111239	NA	NA
Cochlospermaceae	18.036146	NA	NA
Codonaceae	46.700000	NA	NA
Colchicaceae	24.100437	NA	NA
Comandraceae	20.452929	NA	NA
Combretaceae	18.537698	3.045745	8.040984
Commelinaceae	22.817426	NA	NA
Connaraceae	18.671267	NA	NA
Convolvulaceae	27.043628	NA	20.610000
Corallinaceae	24.600000	NA	NA
Cordiaceae	26.773979	NA	22.222748
Coriariaceae	23.145656	NA	NA
Cornaceae	19.015650	NA	7.812801
Corynocarpaceae	30.000000	NA	34.200000
Costaceae	20.694025	NA	NA
Coulaceae	18.024187	NA	NA
Crassulaceae	20.890131	NA	9.510000
Crypteroniaceae	11.190000	NA	NA
Cucurbitaceae	34.184894	NA	NA
Cunoniaceae	11.596341	NA	13.000000
Cupressaceae	11.557371	5.200000	10.299874
Curtisiaceae	14.750000	NA	NA
Cyatheaceae	20.146356	NA	9.750000
Cycadaceae	22.709697	NA	NA
Cyclanthaceae	19.600000	NA	NA
Cyperaceae	19.578327	NA	7.069177
Cyrillaceae	11.676042	NA	NA
Cystopteridaceae	26.087701	NA	NA
Daphniphyllaceae	16.697078	NA	NA
Dennstaedtiaceae	21.009091	NA	NA
Diapensiaceae	11.225000	NA	NA
Dichapetalaceae	16.234979	NA	NA
Dicksoniaceae	14.845833	NA	13.200000
Dicranaceae	6.960000	NA	NA
Didiereaceae	13.800000	NA	NA
Dilleniaceae	13.395289	NA	4.090000
Dioscoreaceae	21.481420	NA	NA
Dipterocarpaceae	16.617894	NA	11.000000
Droseraceae	13.592376	NA	NA
Dryopteridaceae	21.617072	NA	NA
Ebenaceae	17.540189	NA	14.088678
Ehretiaceae	24.178348	NA	NA
Elaeagnaceae	34.198757	NA	28.100000
Elaeocarpaceae	15.733059	NA	13.850000
Ephedraceae	14.259159	NA	NA
Equisetaceae	18.233321	NA	10.919654
Ericaceae	11.965271	2.780000	9.215721
Eriocaulaceae	21.633333	NA	NA
Erythropalaceae	21.326093	NA	NA
Erythroxylaceae	21.484533	NA	NA
Escalloniaceae	18.094942	NA	NA
Euphorbiaceae	25.053831	4.319765	7.033673
Eupteleaceae	21.400000	NA	NA
Fabaceae	28.117544	7.428306	17.968186
Fagaceae	17.363505	7.268250	11.620330
Fissidentaceae	15.100000	NA	NA
Flagellariaceae	24.324811	NA	NA
Fouquieriaceae	13.857143	NA	NA
Garryaceae	13.408563	NA	NA
Gentianaceae	20.818110	NA	NA
Geraniaceae	21.715382	NA	8.446347
Gesneriaceae	21.044023	NA	NA
Ginkgoaceae	19.375000	NA	NA
Gleicheniaceae	12.503416	NA	NA
Gnetaceae	23.623621	NA	NA
Goodeniaceae	12.770560	NA	NA
Goupiaceae	17.470304	NA	NA
Griseliniaceae	9.968742	NA	30.200000
Grossulariaceae	21.745764	NA	12.475793
Gunneraceae	22.700000	NA	NA
Gyrostemonaceae	16.700000	NA	NA
Haematococcaceae	26.810000	NA	NA
Haemodoraceae	35.460000	NA	NA
Haloragaceae	13.066600	NA	NA
Hamamelidaceae	13.017588	NA	11.917021
Heliconiaceae	23.191582	NA	NA
Heliotropiaceae	26.496602	NA	NA
Hemidictyaceae	24.343333	NA	NA
Hernandiaceae	28.683333	NA	NA
Hookeriaceae	11.550000	NA	NA
Humiriaceae	13.643659	NA	NA
Hydrangeaceae	24.405094	NA	NA
Hydrocharitaceae	26.033333	NA	NA
Hydrophyllaceae	34.211537	NA	NA
Hylocomiaceae	8.000000	NA	NA
Hypericaceae	19.973686	NA	NA
Hypoxidaceae	20.550000	NA	NA
Icacinaceae	26.315503	NA	NA
Iridaceae	17.467285	NA	NA
Irvingiaceae	27.566667	NA	NA
Iteaceae	19.533741	NA	NA
Ixerbaceae	7.300000	NA	NA
Ixonanthaceae	18.222880	NA	NA
Juglandaceae	20.948555	NA	NA
Juncaceae	19.689440	NA	8.612483
Juncaginaceae	27.705506	NA	NA
Krameriaceae	19.533354	NA	NA
Lacistemataceae	21.106849	NA	NA
Lamiaceae	22.628692	7.238641	13.011714
Lardizabalaceae	14.882698	NA	12.200000
Lauraceae	19.918654	8.450000	17.581342
Lecythidaceae	21.725974	NA	NA
Lentibulariaceae	19.585904	NA	NA
Lepidobotryaceae	16.734855	NA	NA
Liliaceae	27.279029	NA	NA
Linaceae	19.989866	NA	NA
Lindsaeaceae	30.491111	NA	NA
Loasaceae	13.160000	NA	NA
Loganiaceae	18.399957	NA	NA
Loranthaceae	17.936468	NA	NA
Lycopodiaceae	8.880979	NA	11.162034
Lygodiaceae	35.050000	NA	NA
Lythraceae	16.257492	NA	NA
Magnoliaceae	20.262715	NA	13.491060
Malpighiaceae	22.741160	2.900607	18.996699
Malvaceae	23.035658	7.246698	14.587437
Marantaceae	22.009839	NA	NA
Marattiaceae	25.368000	NA	NA
Marcgraviaceae	12.700000	NA	NA
Mazaceae	25.876667	NA	NA
Melanthiaceae	30.511836	NA	NA
Melastomataceae	18.901019	NA	NA
Meliaceae	25.025835	2.849435	18.080098
Melianthaceae	22.290319	NA	NA
Menispermaceae	20.320352	NA	NA
Menyanthaceae	35.361370	NA	7.084952
Metteniusaceae	13.976361	NA	NA
Molluginaceae	25.736364	NA	NA
Monimiaceae	23.291032	NA	29.500000
Montiaceae	24.054583	NA	NA
Moraceae	21.530594	NA	8.931110
Musaceae	34.583333	NA	NA
Myodocarpaceae	9.800000	NA	NA
Myricaceae	20.594828	NA	13.895174
Myristicaceae	20.059672	NA	NA
Myrtaceae	13.833610	NA	11.460063
Namaceae	29.637748	NA	NA
Nartheciaceae	24.700000	NA	NA
Nelumbonaceae	26.200000	NA	NA
Nephrolepidaceae	16.740417	NA	NA
Nitrariaceae	33.503973	NA	21.340000
Nothofagaceae	14.163151	NA	12.909500
Nyctaginaceae	37.234569	NA	NA
Nymphaeaceae	32.458333	NA	NA
Nyssaceae	14.463636	NA	NA
Ochnaceae	14.940688	NA	NA
Olacaceae	30.456560	NA	NA
Oleaceae	18.699032	2.780000	14.568902
Oleandraceae	16.600000	NA	NA
Onagraceae	23.152644	NA	10.018291
Onocleaceae	25.498562	NA	NA
Ophioglossaceae	32.783960	NA	NA
Opiliaceae	42.403480	NA	NA
Orchidaceae	17.957874	NA	NA
Orobanchaceae	25.757066	NA	NA
Orthotrichaceae	6.080000	NA	NA
Osmundaceae	26.414177	NA	NA
Oxalidaceae	30.182499	NA	NA
Paeoniaceae	19.423601	NA	NA
Pandaceae	34.392599	NA	NA
Pandanaceae	16.656945	NA	NA
Papaveraceae	32.656816	NA	NA
Paracryphiaceae	10.386259	NA	16.200000
Parnassiaceae	17.298686	NA	NA
Passifloraceae	30.295379	NA	NA
Paulowniaceae	15.004442	NA	NA
Pedaliaceae	22.850000	NA	NA
Penaeaceae	18.045000	NA	NA
Pentaphylacaceae	12.533642	NA	NA
Penthoraceae	40.820000	NA	NA
Peraceae	16.848913	NA	NA
Peridiscaceae	13.921055	NA	NA
Phrymaceae	18.115084	NA	NA
Phyllanthaceae	20.024243	NA	NA
Phyllocladaceae	9.113553	NA	14.350000
Phytolaccaceae	36.682157	NA	NA
Picramniaceae	25.729169	NA	NA
Picrodendraceae	15.085556	NA	NA
Pinaceae	12.942295	1.978810	11.012076
Piperaceae	30.478808	NA	NA
Pittosporaceae	12.747401	NA	13.192372
Plagiogyriaceae	23.332250	NA	NA
Plantaginaceae	20.813263	NA	10.781608
Platanaceae	23.238229	NA	NA
Plumbaginaceae	22.717457	NA	7.400000
Poaceae	18.316675	NA	9.301720
Podocarpaceae	11.271467	NA	14.250000
Polemoniaceae	20.570795	NA	NA
Polygalaceae	20.319486	NA	NA
Polygonaceae	28.319115	NA	11.440555
Polypodiaceae	12.511738	NA	NA
Polytrichaceae	11.378150	NA	NA
Pontederiaceae	33.306667	NA	NA
Portulacaceae	20.621667	NA	NA
Potamogetonaceae	38.299866	NA	14.518003
Pottiaceae	15.300000	NA	NA
Primulaceae	16.739662	NA	13.625000
Proteaceae	7.704847	NA	12.426033
Pteridaceae	17.948399	NA	NA
Putranjivaceae	22.615313	NA	7.600000
Quiinaceae	16.384609	NA	NA
Quillajaceae	10.333333	NA	NA
Ranunculaceae	24.728950	NA	12.308324
Resedaceae	35.625000	NA	NA
Restionaceae	8.000000	NA	NA
Rhamnaceae	21.278492	NA	16.700000
Rhizogoniaceae	6.280000	NA	NA
Rhizophoraceae	17.008370	NA	6.400000
Rosaceae	20.490021	NA	11.643586
Rubiaceae	21.408919	NA	14.758185
Rutaceae	24.805269	NA	21.805537
Sabiaceae	14.937467	NA	NA
Salicaceae	23.130763	2.830072	11.972095
Salvadoraceae	26.152886	NA	NA
Santalaceae	10.792099	NA	NA
Sapindaceae	21.286530	4.139490	13.702663
Sapotaceae	19.108913	7.281857	14.795813
Sarcobataceae	16.902834	NA	NA
Sarraceniaceae	9.705030	NA	NA
Saxifragaceae	19.018039	NA	NA
Schisandraceae	15.268439	NA	NA
Schlegeliaceae	8.200000	NA	NA
Schoepfiaceae	28.046620	NA	NA
Scrophulariaceae	18.090465	NA	20.600000
Sematophyllaceae	6.900000	NA	NA
Simaroubaceae	24.803286	NA	11.600000
Simmondsiaceae	16.913670	NA	NA
Siparunaceae	27.322658	NA	NA
Smilacaceae	17.314717	NA	NA
Solanaceae	35.779496	NA	16.605000
Sphagnaceae	8.866667	NA	NA
Staphyleaceae	17.921574	NA	NA
Stemonuraceae	17.489870	NA	NA
Stixaceae	23.666667	NA	NA
Strasburgeriaceae	7.700000	NA	NA
Strombosiaceae	29.209762	NA	NA
Stylidiaceae	12.808803	NA	NA
Styracaceae	16.376992	NA	NA
Symplocaceae	15.478410	NA	NA
Tamaricaceae	21.012878	NA	13.095000
Tapisciaceae	21.542615	NA	NA
Taxaceae	16.422887	NA	NA
Tectariaceae	25.618889	NA	NA
Tetradiclidaceae	19.294690	NA	NA
Theaceae	13.292438	NA	6.300000
Thelypteridaceae	26.939679	NA	NA
Thymelaeaceae	22.203805	NA	NA
Tofieldiaceae	13.727586	NA	NA
Trigoniaceae	25.450000	NA	NA
Typhaceae	23.837149	NA	NA
Ulmaceae	22.750298	NA	23.700000
Urticaceae	25.005457	NA	NA
Velloziaceae	21.096491	NA	NA
Verbenaceae	21.378480	NA	NA
Violaceae	26.430388	NA	18.342843
Viscaceae	26.300000	NA	NA
Vitaceae	23.425993	NA	NA
Vivianiaceae	24.000000	NA	NA
Vochysiaceae	16.407386	NA	NA
Winteraceae	11.822776	NA	13.900000
Ximeniaceae	17.667625	NA	NA
Zamiaceae	18.337149	NA	NA
Zingiberaceae	19.486452	NA	NA
Zygophyllaceae	23.141902	NA	15.277484

When family values are also missing, default tissue-averaged nitrogen concentrations are given: \(N_{leaf} = 20.088\), \(N_{sapwood} = 3.9791\) and \(N_{fineroot} = 12.207\).

Default control values (\(MR_{leaf} = 0.00260274\)), sapwood (\(MR_{sapwood} = 6.849315e-05\)) and fine roots (\(MR_{fineroot} 0.002054795\)) were used in previous model versions, derived from Ogle & Pacala (2009), but these are no longer used because of easier parameterization using tissue nitrogen concentration.

A.3.19 Relative growth rates

When missing at the species parameter table, maximum relative growth rates for leaves, sapwood and fine roots are taken from control parameters. Default values are provided in 15.5.3.

A.3.20 Senescence rates

When missing at the species parameter table, senescence rates for sapwood and fine roots are taken from control parameters.

A.3.21 Relative starch for sapwood growth

When missing at the species parameter table, the minimum relative starch for sapwood growth is taken from control parameters. Default value is provided in 15.5.3.

A.3.22 Wood carbon

Default values for \(C_{wood}\) are determined from taxonomic family using an internal data set (medfate:::trait_family_means):

Table A.8: Default wood carbon content by taxonomic family.

	WoodC
Acanthaceae	0.4242167
Altingiaceae	0.4435000
Amaranthaceae	0.4197662
Amaryllidaceae	0.4508400
Anacardiaceae	0.4566867
Annonaceae	0.4726000
Apiaceae	0.4413076
Apocynaceae	0.4924750
Aquifoliaceae	0.4400000
Araliaceae	0.4540667
Arecaceae	0.4556000
Asparagaceae	0.4631000
Asteraceae	0.4375956
Betulaceae	0.4721962
Bignoniaceae	0.4618077
Boraginaceae	0.4153500
Brassicaceae	0.4274775
Burseraceae	0.4548544
Calophyllaceae	0.4663000
Campanulaceae	0.4498475
Cannabaceae	0.4683583
Caprifoliaceae	0.4475552
Caryophyllaceae	0.4147683
Casuarinaceae	0.4200000
Celastraceae	0.4900000
Chrysobalanaceae	0.4886000
Cistaceae	0.4698925
Clethraceae	0.4400000
Combretaceae	0.4678282
Convolvulaceae	0.4200000
Cordiaceae	0.4652500
Corynocarpaceae	0.4520000
Cupressaceae	0.5006151
Cyperaceae	0.4639737
Dipterocarpaceae	0.4744750
Ebenaceae	0.4828000
Ehretiaceae	0.4500000
Elaeocarpaceae	0.4350000
Ericaceae	0.4865107
Euphorbiaceae	0.4715052
Fabaceae	0.4559793
Fagaceae	0.4642838
Gentianaceae	0.4654867
Geraniaceae	0.4381400
Haematococcaceae	0.4400000
Hypericaceae	0.4547167
Juglandaceae	0.4898900
Juncaceae	0.4238725
Juncaginaceae	0.4056355
Lamiaceae	0.4650444
Lauraceae	0.4677907
Lecythidaceae	0.4618750
Lentibulariaceae	0.4450200
Loganiaceae	0.4943000
Lythraceae	0.4219000
Magnoliaceae	0.4500000
Malpighiaceae	0.4765989
Malvaceae	0.4671722
Melastomataceae	0.4801500
Meliaceae	0.4667281
Moraceae	0.4638776
Muntingiaceae	0.4200000
Myristicaceae	0.4884667
Myrtaceae	0.4270234
Namaceae	0.4700000
Nothofagaceae	0.5225000
Ochnaceae	0.4840000
Oleaceae	0.4748772
Orobanchaceae	0.4437020
Pentaphylacaceae	0.5000000
Phyllanthaceae	0.4668417
Pinaceae	0.4955591
Pittosporaceae	0.4630000
Plantaginaceae	0.4240841
Platanaceae	0.4813333
Plumbaginaceae	0.4353996
Poaceae	0.4362235
Podocarpaceae	0.4700000
Polygalaceae	0.4819000
Polygonaceae	0.4477000
Primulaceae	0.4223568
Quillajaceae	0.4900000
Ranunculaceae	0.4408600
Rhamnaceae	0.4745500
Rhizophoraceae	0.4293500
Rosaceae	0.4407549
Rubiaceae	0.4631136
Rutaceae	0.4718524
Salicaceae	0.4787565
Sapindaceae	0.4755988
Sapotaceae	0.4575714
Schisandraceae	0.4550000
Scrophulariaceae	0.4400000
Simaroubaceae	0.4649167
Solanaceae	0.4325000
Staphyleaceae	0.4490000
Styracaceae	0.4750000
Theaceae	0.4760500
Ulmaceae	0.4859000
Urticaceae	0.4555722
Violaceae	0.4471733
Vochysiaceae	0.4759417

If family-level values are missing, default value of \(C_{wood} = 0.5\,g\,C\cdot g\,dry^{-1}\) is used.

A.3.23 Mortality baseline rate

When missing at the species parameter table, the mortality baseline rate is taken from control parameters. Default value is provided in 15.5.3.

A.3.24 Recruitment

Imputation of missing values for recruitment is specified via control parameters. Default values are provided in 18.4.3.

A.3.25 Flammability

Default values for the surface-area-to-volume ratio (\(\sigma\)), fuel heat content (\(h\)) and lignin percent (\(LI\)) are defined from leaf size and leaf shape as follows:

Leaf shape	Leaf size	\(\sigma\)	\(h\)	\(LI\)
Broad	Large	5740	19740	15.50
Broad	Medium	4039	19825	20.21
Broad	Small	4386	20062	22.32
Linear/Needle	Large	3620	18250	24.52
Linear/Needle	Medium	4758	21182	24.52
Linear/Needle	Small	6697	21888	18.55
Spines	[any]	6750	20433	14.55
Scale	[any]	1120	20504	14.55

Default value for the density of fuel particles (\(\rho_p\)) is 400 \(kg\cdot m^{-3}\).

A.4 Scaling size-related parameters

A.4.1 Stem xylem maximum conductance

Estimation of maximum stem conductance (\(k_{s,max}\), in \(mmol \cdot m^{-2} \cdot s^{-1} \cdot MPa^{-1}\)) is done by function hydraulics_maximumStemHydraulicConductance() and follows the work by Savage et al. (2010), Olson et al. (2014) and Christoffersen et al. (2016). Calculations are based on tree height and two species-specific parameters: maximum sapwood reference conductivity (\(K_{s,max,ref}\)) and the ratio of leaf area to sapwood area (\(A_{l}/A_{s}\); Al2As in SpParamsMED), i.e. the inverse of the Huber value \(H_v\).

The reference value for maximum sapwood conductivity \(K_{s,max,ref}\) is assumed to have been measured on a terminal branch of a plant of known height \(H_{ref}\). If our target plant is very different in height, the conduits of terminal branches will have different radius and hence conductivity. We correct the reference conductivity to the target plant height using the following empirical relationship, developed by Olson et al. (2014) between tree height and diameter of conduits for angiosperms and the equation described by Christoffersen et al. (2016): \[\begin{eqnarray} 2 \cdot r_{int,H}&=& 10^{1.257+(0.24\cdot log_{10}(H))} \\ 2 \cdot r_{int,ref}&=&10^{1.257+(0.24\cdot log_{10}(H_{ref}))}\\ K_{s,max,cor}&=&K_{s,max,ref}\cdot (r_{int,H}/r_{int,ref})^{2} \end{eqnarray}\] Where \(r_{int,H}\) is the radius of conduits for a terminal branch of a tree of height \(H\) and \(r_{int,ref}\) is the corresponding radius for a tree of height \(H_{ref}\) (\(H\) and \(H_{ref}\) are measured in m). The form of the empirical relationship by Olson et al. (2014) is:

Let’s consider an example for a Quercus ilex target tree of 4m height and where species-specific conductivity \(K_{s,max,ref} = 0.77\) is the apical value for trees of \(H_{ref} = 6.6\) m (in , values of \(H_{ref}\) are taken from median height values; see parameter Hmed in SpParamsMED). The corrected conductivity for a tree of height 4 m will be a bit lower than that of the reference height:

xylem_kmax = 0.77
H = 400 # in cm
Href = 660 # in cm
f = hydraulics_referenceConductivityHeightFactor(Href, H);
f

## [1] 0.7863352

xylem_kmax_cor = xylem_kmax * f
xylem_kmax_cor

## [1] 0.6054781

Once the reference conductivity is corrected, the maximum stem conductance without accounting for conduit taper is: \[\begin{equation} k_{s,max, notaper}=\frac{1000}{0.018} \frac{K_{s,max,cor}\cdot A_{s}}{H\cdot A_{l}} \end{equation}\] where \(H\) is the tree height (here in m), \(A_{s}\) is the sapwood area, \(A_{l}\) is the leaf area and 1000/0.018 is a factor used to go from kg to mmol. The ratio \(A_{l}/A_{s} = 1/H_v\) is a fixed species parameter in soil water balance calculations (see parameter Al2As), but becomes variable when simulating plant growth. Let’s assume that Quercus ilex the leaf to sapwood area ratio is \(A_{l}/A_{s} = 2512\). The maximum (leaf-specific) stem conductance without taper (\(k_{s, max, notaper}\)) for the tree of 4 m height is then:

Al2As = 2512 

kstemmax = hydraulics_maximumStemHydraulicConductance(xylem_kmax, 
                  Href, Al2As, H, taper = FALSE)
kstemmax

## [1] 3.347698

In order to consider taper of xylem conduits we calculate the whole-tree conductance per unit leaf area (\(k_{s, max, taper}\)) as described in Christoffersen et al. (2016): \[\begin{equation} k_{s, max, taper}=\frac{1000}{0.018} \cdot \frac{K_{s,max,pet}\cdot A_{s}}{H\cdot A_{l}}\cdot \chi_{tap:notap,ag}(H) \end{equation}\] where \(K_{s,max,pet}\) is the conductivity at the petiole level and \(\chi_{tap:notap,ag}(H)\) is the taper factor accounting for the decrease in the xylem conduits diameter with the height, from the petiole to base of the trunk, which mitigates the negative effects of height on the hydraulic safety. The conductivity at the petiole level is obtained from \(K_{s,max,ref}\) using again: \[\begin{equation} K_{s,max,pet} = K_{s,max,ref}\cdot (r_{int, pet}/r_{int,ref})^{2} \end{equation}\] where \(r_{int, pet}\) is the radius of the petiole in the model of Savage et al. (2010). Christoffersen et al. (2016) use \(r_{int, pet} = 10\) \(\mu m\) but we define it as the radius of apical conduits in a tree of 1 m height:

hydraulics_terminalConduitRadius(100.0)

## [1] 9.035871

\(\chi_{tap:notap,ag}(H)\) is calculated as described in the Appendix 1 section of Christoffersen et al. (2016) (see also Savage et al. (2010)). The following figure shows the value of \(\chi_{tap:notap,ag}\) for different heights:

Note that, since \(\chi_{tap:notap,ag}(1) = 3.82\) (indicated using grey dashed lines in the last figure), the equation of maximum conductance with taper would give a higher conductance than the equation without taper for a tree of 1 m height, which is supposed to have a conductance equal to conductivity. To solve this issue we define the taper factor as \(\chi_{tap:notap,ag}(H)/\chi_{tap:notap,ag}(1)\): \[\begin{equation} k_{s, max, taper}=\frac{1000}{0.018} \cdot \frac{K_{s,max,pet}\cdot A_{s}}{H\cdot A_{l}}\cdot \frac{\chi_{tap:notap,ag}(H)}{\chi_{tap:notap,ag}(1)} \end{equation}\] The maximum stem conductance with taper (\(k_{s, max, taper}\)) of a Q. ilex tree of 4 m height, calculated with this second equation, is:

kstemmax_tap = hydraulics_maximumStemHydraulicConductance(xylem_kmax, 
                      Href, Al2As, H, taper = TRUE)
kstemmax_tap

## [1] 4.764396

The next two plots show the variation of \(k_{s,max}\) for Q. ilex depending on the tree height and with/without considering taper of conduits. The plot on the right (both axes in log) show the slope of the dependency of conductance with height in both cases:

A.4.2 Leaf maximum hydraulic conductance

A.4.3 Root xylem maximum hydraulic conductance

To obtain maximum root xylem conductance (\(k_{r, max}\), in \(mmol \cdot m^{-2} \cdot s^{-1} \cdot MPa^{-1}\)), one option taken by Christoffersen et al. (2016) is to assume that minimum stem resistance (inverse of maximum conductance) represents a fixed proportion of the minimum total tree (stem+root) resistance. A value 0.625 (i.e. 62.5%) suggested by these authors leads to maximum total tree conductance for our Q. ilex tree being:

ktot = kstemmax*0.625
ktot

## [1] 2.092311

and the maximum root xylem conductance would be therefore:

krootmax = 1/((1/ktot)-(1/kstemmax))
krootmax

## [1] 5.579497

Now, we need to divide total maximum conductance of the root system xylem among soil layers we need weights inversely proportional to the length of transport distances (Sperry et al. 2017). Vertical transport lengths can be calculated from soil depths and radial spread can be calculated assuming cylinders with volume proportional to the proportions of fine root biomass. Let’s assume a soil with three layers:

s <- soil(defaultSoilParams(3))
d <- s$widths
d

## [1]  300  700 1000

The proportion of fine roots in each layer, assuming a linear dose response model, will be:

Z50 <- 200
Z95 <- 1500
v1 <- root_ldrDistribution(Z50,Z95, NA, d)
v1

##           [,1]      [,2]       [,3]
## [1,] 0.6661036 0.2784153 0.05548106

Having this information, the calculation of root length (i.e. the sum of vertical and radial lengths) to each layer (\(L_j\)) is done using function root_coarseRootLengths():

rfc <- c(20,50,70)
Vol <- root_coarseRootSoilVolumeFromConductance(1.0, 2500,krootmax,
                                               v1, d, rfc)
l <- root_coarseRootLengthsFromVolume(Vol, v1, d, rfc)
l

## [1] 4503.445 3250.363 3085.055

where lengths are in mm. The proportion of total root xylem conductance corresponding to each layer (\(w_j\)) is given by root_xylemConductanceProportions():

w1 <- hydraulics_rootxylemConductanceProportions(v1, l)
w1

## [1] 0.09131268 0.15767645 0.75101087

Xylem conductance proportions can be quite different than the fine root biomass proportions. This is because radial lengths are largest for the first top layers and vertical lengths are largest for the bottom layers. The maximum root xylem conductances of each layer will be the product of maximum total conductance of root xylem and weights:

w1*krootmax

## [1] 0.5094788 0.8797553 4.1902629

The maximum root xylem conductances of each layer would be:

krootmaxvec = w1*krootmax
krootmaxvec

## [1] 0.5094788 0.8797553 4.1902629

and the fraction of total xylem resistance due to stem would be:

(1/kstemmax)/((1/kstemmax)+(1/krootmax))

## [1] 0.625

In contrast with the approach of Christoffersen et al. (2016), in this approach the root maximum conductance depends root length and distribution, and is not a fixed fraction of stem maximum conductance. Assuming constant root length, then the proportion of total resistance due to the stem will increase with tree height (Magnani et al. 2000):

where the horizontal gray line indicates the value of 62.5%. Of course rooting depth also increases with tree age, but young trees have higher root-to-shoot ratios than older ones. Hence, a root maximum conductance that is not fixed but increases with age seems a priori more realistic. Moreover, Christoffersen et al. (2016) justify the value of 62.5% from a study which quantified total aboveground and belowground resistance in tropical trees (Fisher et al. 2006) under near-saturated (wet season) conditions, but values of belowground resistance reported in this study for wet conditions and trees of 30 m height are around 13%, which equals to 87% fraction of aboveground resistance. On the other hand, while rooting depths are limited by soil depth, lateral root length increases with age and, hence, the model could be made more realistic if this is taken into account and the curve above would probably saturate at lower percentages.

A.4.4 Rhizosphere maximum hydraulic conductance

Maximum rhizosphere conductance (\(k_{rh, max}\), in \(mmol \cdot m^{-2} \cdot s^{-1} \cdot MPa^{-1}\)) is difficult to measure directly, as it depends on the rhizosphere (i.e. fine root) surface in each soil layer, and will probably always be a parameter to be calibrated. Instead of trying to estimate rhizosphere surface from root architecture (Sperry et al. 1998), we follow Sperry et al. (2016) and determine the maximum rhizosphere conductance in each layer from an inputed ‘average percentage rhizosphere resistance’. The percentage of continuum resistance corresponding to the rhizosphere is calculated from the vulnerability curves of stem, root and rhizosphere at the same water potential. The average resistance is found by evaluating the percentage for water potential values between 0 and \(\Psi_{crit}\). The following figure illustrates how the supply function, for different soil water potentials, is affected by increasing values of the average percentage of rhizosphere resistance:

Sperry et al. (2016) found average percentages of rhizosphere resistance around 67%, but these exceptionally-high values were probably a consequence of using an unsegmented supply function (i.e. single vulnerability curve for roots, stem and leaves). If we specify a 15% of average resistance in the rhizosphere (see parameter averageFracRhizosphereResistance in function defaultControl()), the maximum rhizosphere conductance values for the three layers are found calling:

krmax = rep(0,3) 
krmax[1]= hydraulics_findRhizosphereMaximumConductance(15, 
                     s$VG_n[1],s$VG_alpha[1],
                     krootmax, rootc,rootd, 
                     kstemmax, stemc, stemd,
                     kleafmax, leafc, leafd)
krmax[2] = hydraulics_findRhizosphereMaximumConductance(15, 
                      s$VG_n[2],s$VG_alpha[2],
                      krootmax, rootc,rootd, 
                      kstemmax, stemc, stemd,
                      kleafmax, leafc, leafd)
krmax[3] = hydraulics_findRhizosphereMaximumConductance(15, 
                      s$VG_n[3],s$VG_alpha[3],
                      krootmax, rootc,rootd, 
                      kstemmax, stemc, stemd,
                      kleafmax, leafc, leafd)
krmax

## [1] 85636744 85636744 85636744

The values are the same because the texture of the three layers is the same in this case. If we take into account root distribution, actual maximum rhizosphere conductance values are:

krmax*v1

##          [,1]     [,2]    [,3]
## [1,] 57042945 23842581 4751218

A.4.5 Plant water storage capacity

The water storage capacity of sapwood tissue per leaf area unit (\(V_{sapwood}\); in \(l \cdot m^{-2}\)) can be estimated as the product of stem height (\(H\) in m) and Huber value (\(H_v\); ratio of sapwood area to leaf area in \(m^2 \cdot m^{-2}\)) times a factor to account for the non-cylindrical shape (http://www.fao.org/forestry/17109/en/): \[\begin{equation} V_{sapwood} = 10^3 \cdot 0.48 \cdot H \cdot H_v \cdot \Theta_{sapwood} \end{equation}\] \(\Theta_{sapwood}\) is sapwood porosity (\(cm^3\) of water per \(cm^3\) of sapwood tissue), which can be estimated from wood density (\(\rho_{wood}\); in \(g \cdot cm^{-3}\)): \[\begin{equation} \Theta_{sapwood} = 1 - (\rho_{wood} / 1.54) \end{equation}\] where the density of wood substance can be assumed to be fixed and equal to 1.54 \(g \cdot cm^{-3}\) (Dunlap 1914). For example, wood densities ranging from 0.443 to 1.000 \(g \cdot cm^{-3}\) result in sapwood porosity values between 0.35 and 0.71.

Water storage capacity of leaf tissue per leaf area unit (\(V_{leaf}\); in \(l \cdot m^{-2}\)) can be estimated as the product of specific leaf area (SLA; in \(m^2 \cdot kg^{-1}\)) and leaf density (\(\rho_{leaf}\); in \(g \cdot cm^{-3}\)): \[\begin{equation} V_{leaf} = \frac{1}{SLA \cdot \rho_{leaf}} \cdot \Theta_{leaf} \end{equation}\] \(\Theta_{leaf}\) is leaf porosity (\(cm^3\) of water per \(cm^3\) of leaf tissue), which can be estimated from leaf density: \[\begin{equation} \Theta_{leaf} = 1 - (\rho_{leaf} / 1.54) \end{equation}\] where the density of wood substance can be assumed to be fixed and equal to 1.54 \(g \cdot cm^{-3}\) (Dunlap 1914).

For example, let’s calculate the stem and leaf water capacity for a Q. ilex tree of 15 m height:

ld = 0.7
SLA = 5.870 
moisture_leafWaterCapacity(SLA, ld)

## [1] 0.1327463

A.4.6 Horizontal root overlap

A.4.6.1 Basic water balance

A given plant cohort \(i\) will have its roots in layer \(s\) partitioned among different water pools. We thus need to define \(fr_{i,s,j}\), the (horizontal) proportion of fine roots of cohort \(i\) in layer \(s\) of the water pool \(j\), with the restriction that: \[\begin{equation} \sum_{j}{fr_{i,s,j}} = 1 \,\, \forall i,s \end{equation}\] It is important to realize that proper estimation of \(fr_{i,s,j}\) is challenging when we do not have explicit plant coordinates, root lateral widths, etc. For this reason, an intuitive approach is followed here based on the following two premises:

• The amount of overlap between roots of different plants should monotonically increase along with the LAI of the stand (i.e. \(LAI^{live}_{stand}\)).
• The amount of overlap between roots of different plants at a given soil depth should increase/decrease with the vertical proportion of roots at that depth.

The specific formulation we chose for \(fr_{i,s,j}\) is: \[\begin{equation} fr_{i,s,j} = f_{pool,j} \cdot (1 - \exp(- f_{overlap} \cdot LAI^{live}_{stand})) \cdot \left( \frac{\sqrt{FRP_{i,s} \cdot FRP_{j,s}}}{\max_{s}(FRP_{i,s})} \right) \end{equation}\] for all \(j \neq i\), where \(f_{overlap}\) is an overlap factor (a control parameter called poolOverlapFactor). For \(j=i\) then we simply have: \[\begin{equation} fr_{i,s,i} = 1 - \sum_{j}{fr_{i,s,j}} \end{equation}\] Note that if \(f_{overlap} = 0\) then \(fr_{i,s,j} = 1\) if \(j=i\) and zero otherwise (i.e. plants exploit their corresponding water pools only. For very large values of \(LAI^{live}_{stand}\) and/or \(f_{overlap}\) we have that \((1 - \exp(- f_{overlap} \cdot LAI^{live}_{stand})) = 0\) and \(fr_{i,s,j} = f_{pool,j}\) (neglecting vertical differences), so that plants exploit the each water pool in the same proportion as the fraction of stand occupied by the pool (i.e. overlap is maximum).

Bibliography

Bartlett, M.K., Klein, T., Jansen, S., Choat, B. & Sack, L. (2016). The correlations and sequence of plant stomatal, hydraulic, and wilting responses to drought. Proceedings of the National Academy of Sciences of the United States of America, 113, 13098–13103.

Bartlett, M.K., Scoffoni, C. & Sack, L. (2012). The determinants of leaf turgor loss point and prediction of drought tolerance of species and biomes: A global meta-analysis. Ecology letters, 15, 393–405.

Choat, B., Jansen, S., Brodribb, T.J., Cochard, H., Delzon, S., Bhaskar, R., et al. (2012). Global convergence in the vulnerability of forests to drought. Nature, 491, 752–755.

Christoffersen, B.O., Gloor, M., Fauset, S., Fyllas, N.M., Galbraith, D.R., Baker, T.R., et al. (2016). Linking hydraulic traits to tropical forest function in a size-structured and trait-driven model (TFS v.1-Hydro). Geoscientific Model Development Discussions, 9, 4227–4255.

De Cáceres, M., Casals, P., Gabriel, E. & Castro, X. (2019). Scaling-up individual-level allometric equations to predict stand-level fuel loading in Mediterranean shrublands. Annals of Forest Science, 76, 87.

Delpierre, N., Dufrêne, E., Soudani, K., Ulrich, E., Cecchini, S., Boé, J., et al. (2009). Modelling interannual and spatial variability of leaf senescence for three deciduous tree species in France. Agricultural and Forest Meteorology, 149, 938–948.

Dunlap, F. (1914). Density of wood substance and porosity of wood. Journal of Agricultural Research, II, 423–428.

Duursma, R.A., Blackman, C.J., Lopéz, R., Martin-StPaul, N.K., Cochard, H. & Medlyn, B.E. (2018). On the minimum leaf conductance: Its role in models of plant water use, and ecological and environmental controls. New Phytologist, 221, 693–705.

Fisher, R.A., Williams, M., Do Vale, L.R., Da Costa, A.L. & Meir, P. (2006). Evidence from Amazonian forests is consistent with a model of isohydric control of leaf water potential. Plant, Cell and Environment, 29, 151–165.

Franks, P.J. (2006). Higher rates of leaf gas exchange are associated with higher leaf hydrodynamic pressure gradients. Plant, Cell and Environment, 29, 584–592.

Granier, A., Bréda, N., Biron, P. & Villette, S. (1999). A lumped water balance model to evaluate duration and intensity of drought constraints in forest stands. Ecological Modelling, 116, 269–283.

Hoshika, Y., Osada, Y., Marco, A. de, Peñuelas, J. & Paoletti, E. (2018). Global diurnal and nocturnal parameters of stomatal conductance in woody plants and major crops. Global Ecology and Biogeography, 27, 257–275.

Magnani, F., Mencuccini, M. & Grace, J. (2000). Age-related decline in stand productivity: The role of structural acclimation under hydraulic constraints. Plant, Cell and Environment, 23, 251–263.

Maherali, H., Pockman, W. & Jackson, R. (2004). Adaptive variation in the vulnerability of woody plants to xylem cavitation. Ecology, 85, 2184–2199.

Ogle, K. & Pacala, S.W. (2009). A modeling framework for inferring tree growth and allocation from physiological, morphological and allometric traits. Tree Physiology, 29, 587–605.

Oliveras, I., Martínez-Vilalta, J., Jimenez-Ortiz, T., Lledó, M.J., Escarré, A. & Piñol, J. (2003). Hydraulic architecture of Pinus halepensis, P . Pinea and Tetraclinis articulata in a dune ecosystem of Eastern Spain. Plant Ecology, 131–141.

Olson, M.E., Anfodillo, T., Rosell, J.A., Petit, G., Crivellaro, A., Isnard, S., et al. (2014). Universal hydraulics of the flowering plants: Vessel diameter scales with stem length across angiosperm lineages, habits and climates. Ecology Letters, 17, 988–997.

Plavcová, L. & Jansen, S. (2015). The Role of Xylem Parenchyma in the Storage and Utilization of Nonstructural Carbohydrates. In: Functional and Ecological Xylem Anatomy. Springer International Publishing, Cham, pp. 209–234.

Reich, P.B., Tjoelker, M.G., Pregitzer, K.S., Wright, I.J., Oleksyn, J. & Machado, J.L. (2008). Scaling of respiration to nitrogen in leaves, stems and roots of higher land plants. Ecology Letters, 11, 793–801.

Savage, V.M., Bentley, L.P., Enquist, B.J., Sperry, J.S., Smith, D.D., Reich, P.B., et al. (2010). Hydraulic trade-offs and space filling enable better predictions of vascular structure and function in plants. Proceedings of the National Academy of Sciences of the United States of America, 107, 22722–7.

Sperry, J.S., Adler, F.R., Campbell, G.S. & Comstock, J.P. (1998). Limitation of plant water use by rhizosphere and xylem conductance: Results from a model. Plant, Cell & Environment, 21, 347–359.

Sperry, J.S., Venturas, M.D., Anderegg, W.R.L., Mencuccini, M., Mackay, D.S., Wang, Y., et al. (2017). Predicting stomatal responses to the environment from the optimization of photosynthetic gain and hydraulic cost. Plant, Cell & Environment, 40, 816–830.

Sperry, J.S., Wang, Y., Wolfe, B.T., Mackay, D.S., Anderegg, W.R.L., Mcdowell, N.G., et al. (2016). Pragmatic hydraulic theory predicts stomatal responses to climatic water deficits. New Phytologist, 212, 577–589.

Walker, A.P., Beckerman, A.P., Gu, L., Kattge, J., Cernusak, L.A., Domingues, T.F., et al. (2014). The relationship of leaf photosynthetic traits - Vcmax and Jmax - to leaf nitrogen, leaf phosphorus, and specific leaf area: A meta-analysis and modeling study. Ecology and Evolution, 4, 3218–3235.