Chapter 12 Stomatal regulation, transpiration and photosynthesis
Plants must open their stomata to acquire \(CO_2\) and perform photosynthesis, but doing so promotes water loss. This trade-off has resulted in a tight coordination between capacity to supply and transpire water (hydraulic conductance and diffusive conductance to water vapor) and the maximum capacity for photosynthesis (carboxylation rate and electron-transport rate). For modelling purposes, this carbon-for-water trade-off means that hydraulics, stomatal conductance, transpiration and photosynthesis need to be estimated simultaneously. In chapters 10 and 11 we introduced plant hydraulics and photosynthesis, respectively, but we did not explain how are actual transpiration and photosynthesis values determined. This depends on the sub-model chosen and is the subject of the present chapter.
12.1 Stomatal regulation under Sperry’s sub-model
The framework of Sperry et al. (2017) suggests estimating stomatal conductance from the instantaneous maximization of profit, defined as the difference between photosynthesis gain and hydraulic cost (both normalized for comparability). First, transpiration and photosynthesis is estimated separately for sunlit and shade leaves according to this framework. An average transpiration rate is then determined depending on sunlit/shade transpiration rates and their leaf area contributions. Finally, the instantaneous transpiration and assimilation rates of each time step are scaled to the duration of the time step and to the leaf area of the plant cohort. The following sections provide details for all these steps.
12.1.1 Water supply and sunlit/shade photosynthesis functions
Let us start by summarizing the concepts introduced in the last two chapters. The supply function described in chapter 10 describes the rate of transpiration flow as a function of the pressure drop between the soil and the leaf, and incorporates both soil, xylem and leaf hydraulic constrains (Sperry et al. 1998, 2016; Sperry & Love 2015). Here we assume that hydraulic conductance \(k\) is in \(mmol\,H_2O \cdot s^{-1} \cdot m^{-2}\cdot MPa^{-1}\) of leaf area, transpiration rate \(E_{leaf}\) in \(mmol\,H_2O \cdot s^{-1} \cdot m^{-2}\) of leaf area and leaf water potential \(\Psi_{leaf}\) is in MPa.
According to section 11.1, each \(E_{leaf}\) value implies an energy balance at the leaf level, stomatal conductance to water vapour and a particular value of leaf photosynthesis. More specifically, for each pair of \(E_{leaf}\) and \(\Psi_{leaf}\) values, we have a corresponding leaf temperature (\(T_{leaf}\); in ºC), leaf-to-air vapor pressure deficit (\(VPD_{leaf}\); in kPa), leaf water vapor conductance (\(g_{sw}\); in \(mol\,H_2O·s^{-1}·m^{-2}\)) and, finally the leaf gross and net (i.e. after accounting for autotrophic respiration) photosynthesis assimilation rates (\(A_g\) and \(A_n\); both in \(\mu mol\,CO_2·s^{-1}·m^{-2}\)). In short, the supply function generates a photosynthesis function. Since the model deals with canopies and not single leaves, however, different parts of the crowns of plant cohorts may be in different canopy positions. Calculating photosynthesis at the canopy level requires dividing the canopy into vertical layers, differentiating between sunlit and shade leaves and determining photosynthesis functions for sunlit and shade leaves separately, as explained in section 11.2.
12.1.2 Leaf stomatal regulation by profit maximization
Wolf et al. (2016) proposed the carbon maximization criterion, which states that at each instant in time the stomata regulate canopy gas exchange and pressure to achieve the maximum profit, which is the maximum difference between photosynthetic gains and costs, the latter associated with hydraulic vulnerability attained with low water potentials. Such approach has been shown to be supported by data from global forest biomes (Anderegg et al. 2018). Building on this approach, Sperry et al. (2017) presented a profit maximization function where hydraulic costs of opening the stomata are compared against photosynthetic gains. Details of their formulation are given in this section. Stomatal regulation is performed in medfate separatedly for sunlit and shade leaves.
12.1.2.1 Cost and gain functions
The hydraulic supply function is used to derive a transpirational cost function \(\theta_1(\Psi_{leaf})\) that reflects the increasing damage from cavitation and the greater difficulty of moving water along the continuum (Sperry et al. 2016): \[\begin{equation} \theta(\Psi_{leaf}) = \frac{k_{c,max}-k_{c}(\Psi_{leaf})}{k_{c,max}-k_{crit}} \end{equation}\] where \(k_c(\Psi_{leaf}) = dE/d\Psi(\Psi)\) is the slope of the supply function corresponding to (leaf) water potential \(\Psi_{leaf}\), \(k_{c,max}\) is the maximum slope of the supply function (which occurs when \(E_{leaf}=0\)), i.e. the maximum whole-plant conductance for the current soil moisture conditions, and \(k_{crit} = k_c(\Psi_{crit})\) is the slope of the supply function at \(E_{leaf} = E_{crit}\) the critical flow beyond which hydraulic failure occurs.
The following figures illustrate the \(\theta(\Psi_{leaf})\) curves corresponding to the supply functions:
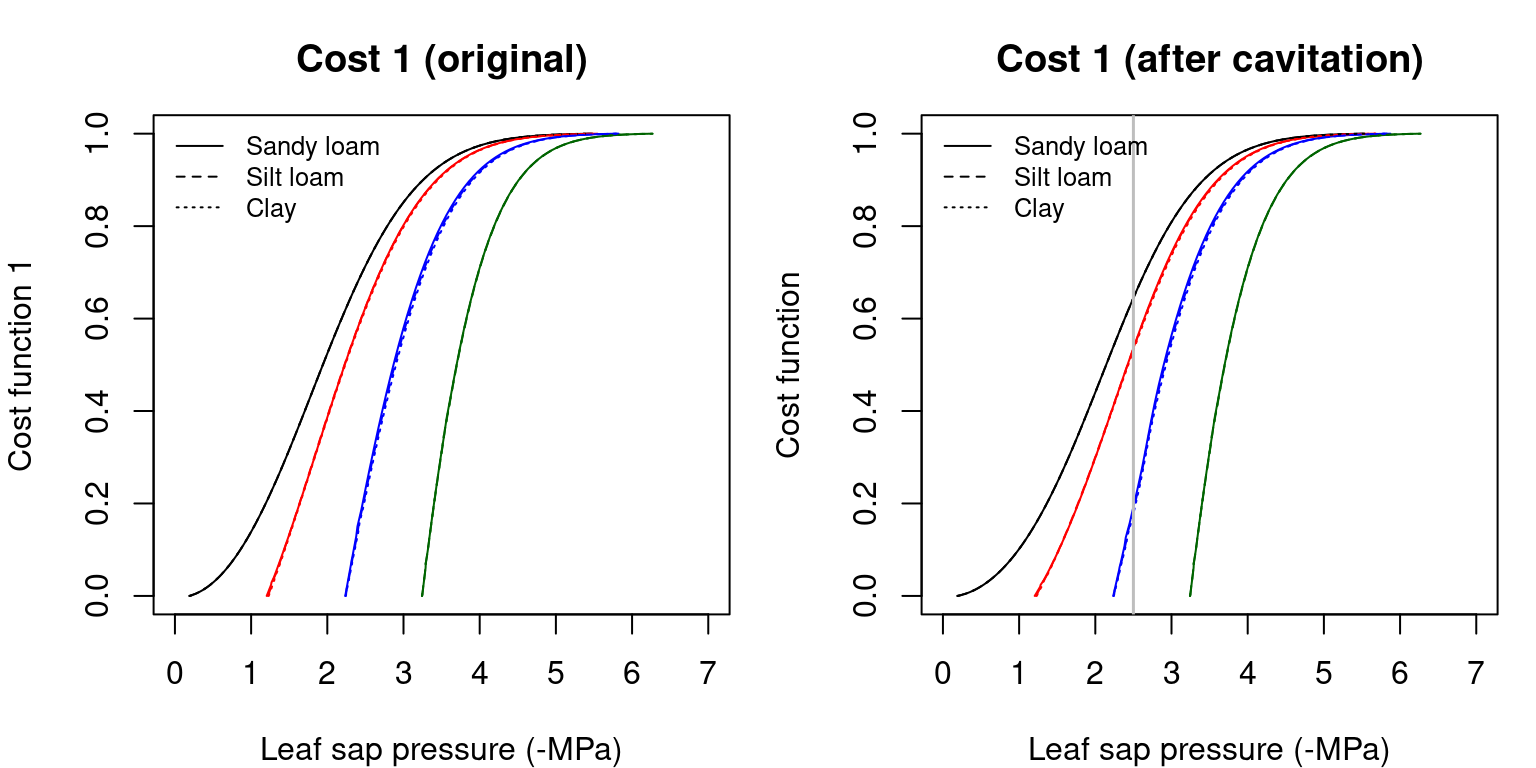
Figure 12.1: Cost functions (i.e. \(\theta(\Psi_{leaf})\)) obtained for a hydraulic network, corresponding to fig. 10.15 and different soil textures and soil water potentials. Left/right panels show values for uncavitated/cavitated supply functions, respectively.
The normalized photosynthetic gain function \(\beta(\Psi_{leaf})\) reflects the actual assimilation rate with respect to the maximum (Sperry et al. 2016): \[\begin{equation} \beta(\Psi_{leaf}) = \frac{A(\Psi_{leaf})}{A_{max}} \end{equation}\] where \(A_{max}\) is the instantaneous maximum (gross) assimilation rate estimated over the full \(\Psi_{leaf}\) range (including values that imply a stomatal conductance larger than the maximum).
The following figures illustrate the \(\beta(\Psi_{leaf})\) curves corresponding to the supply and assimilation functions:
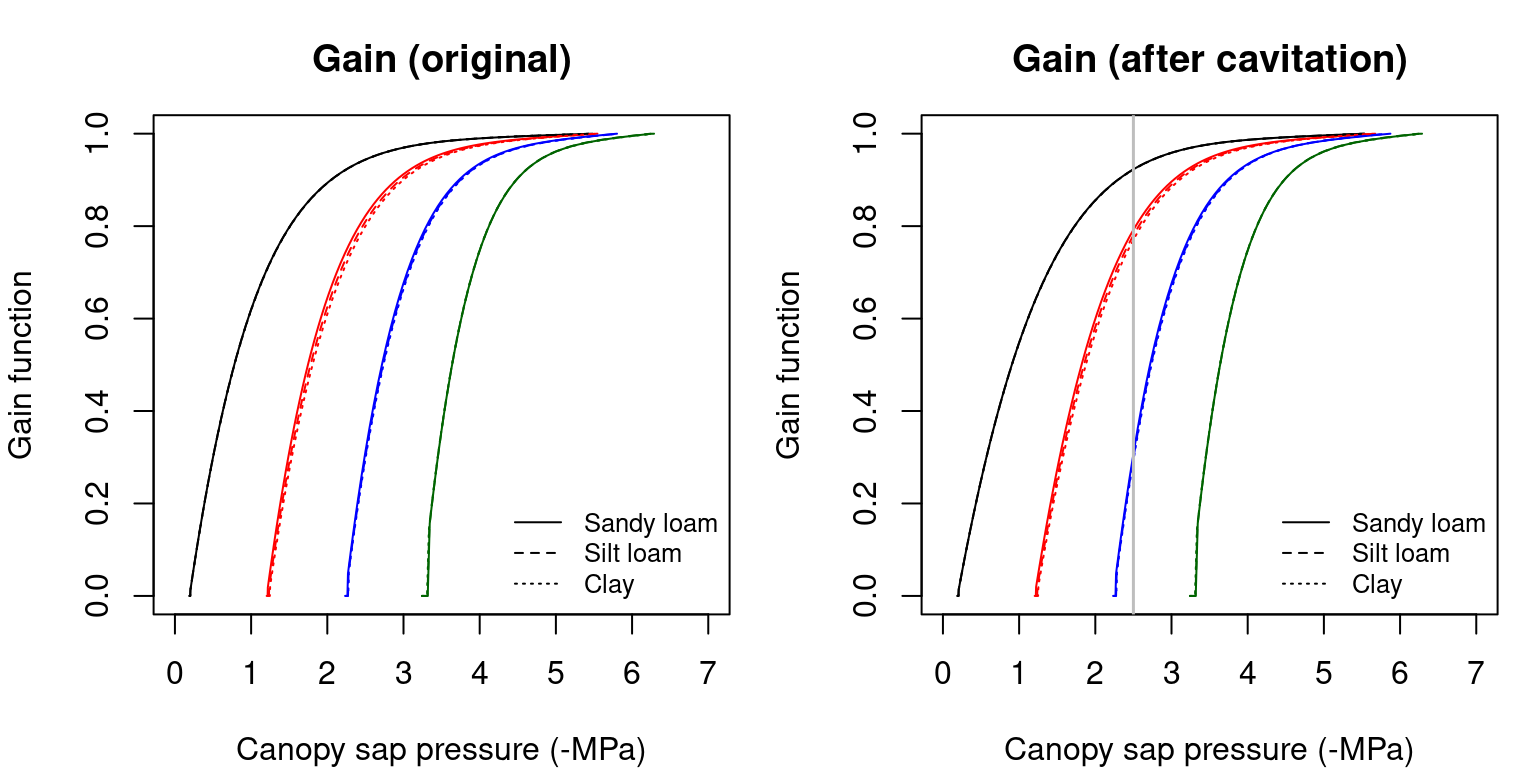
Figure 12.2: Gain function (\(\beta(\Psi_{leaf})\)) obtained for a hydraulic network, corresponding to fig. 10.15 and different soil textures and soil water potentials. Left/right panels show values for uncavitated/cavitated supply functions, respectively.
12.1.2.2 Profit maximization at the leaf level
Sperry et al. (2017) suggested that stomatal regulation can be effectively estimated by determining the maximum of the profit function (\(Profit(\Psi_{leaf})\)): \[\begin{equation} Profit(\Psi_{leaf}) = \beta(\Psi_{leaf})-\theta(\Psi_{leaf}) \end{equation}\] The maximization is achieved when the slopes of the gain and cost functions are equal: \[\begin{equation} \frac{\delta \beta(\Psi_{leaf})}{\delta \Psi_{leaf}} = \frac{\delta \theta(\Psi_{leaf})}{\delta \Psi_{leaf}} \end{equation}\] Instantaneous profit maximization assumes a ‘use it or lose it’ reality with regards to available soil water. Because the gain function accelerates more quickly from zero and reaches 1 sooner than the cost functiion, their maximum difference occurs at intermediate \(\Psi_{leaf}\) values. Once \(\Psi_{leaf}\) that maximizes profit is determined, the values of the remaining variables are also determined. At this point, it may happen that \(g_{sw}(\Psi_{leaf})\) is lower than the minimum (i.e. cuticular) water vapor conductance (\(g_{sw,\min}\)) or larger than the maximum water vapor conductance (\(g_{sw,\max}\)). These thresholds need to be taken into account when determining the maximum of the profit function.
The following figures illustrate the \(Profit(\Psi_{leaf})\) curves of corresponding to the previous cost and gain curves:
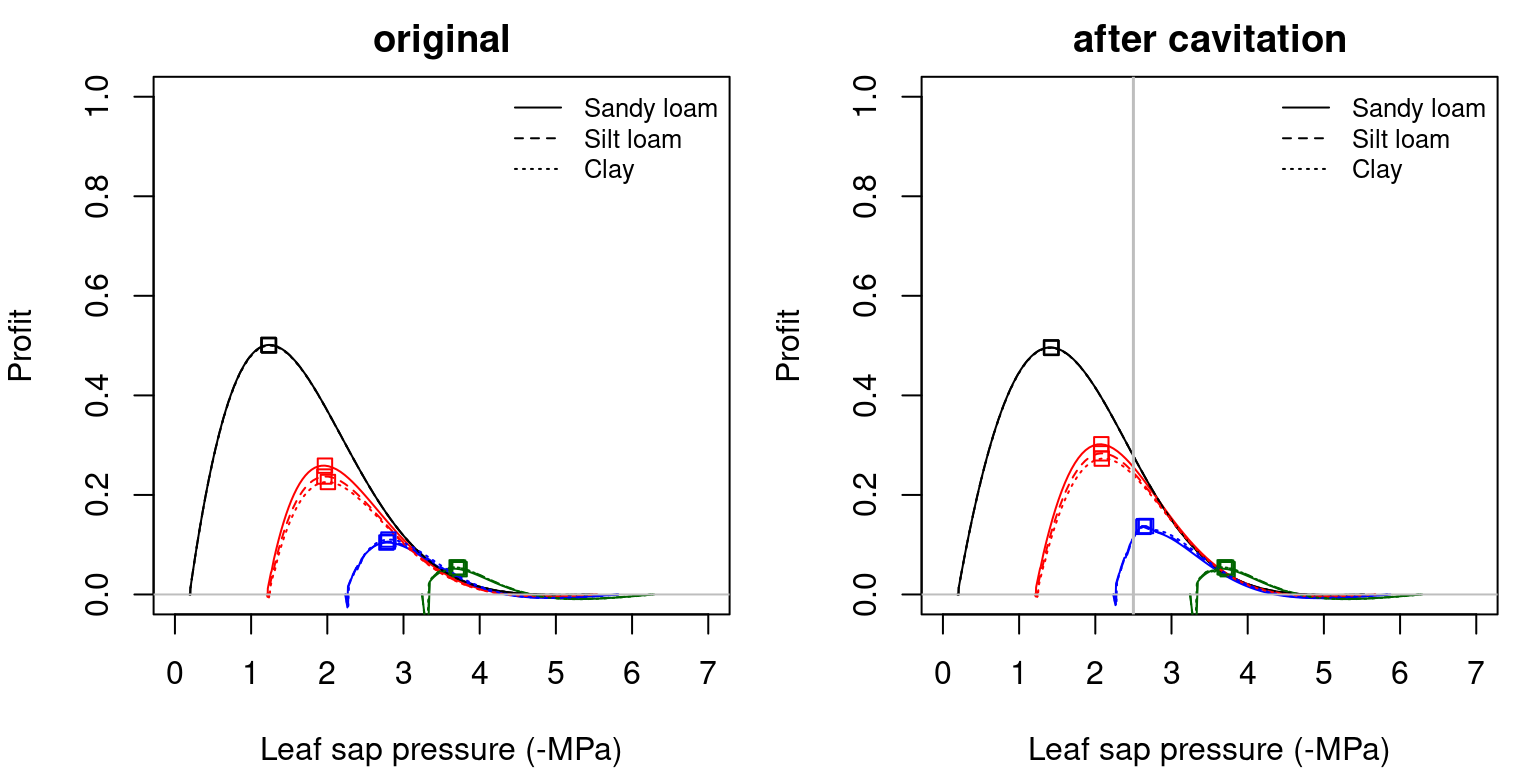
Figure 12.3: Profit functions (i.e. \(Profit(\Psi_{leaf})\)) obtained for a hydraulic network, corresponding to fig. 10.15 and different soil textures and soil water potentials. Left/right panels show values for uncavitated/cavitated supply functions, respectively.
Squares in the previous figures indicate the maximum profit points in each situation. The drier the soil, the closer is the maximum profit \(\Psi_{leaf}\) to soil water potential as one would expect intuitively (i.e. a smaller drop in water potential along the hydraulic pathway). Note that when the soil is very dry the squares are to the right of the true maximum. This is because the transp_profitMaximization() function takes into account the minimum and maximum stomatal conductance and, in this case, does not allow optimum stomatal conductances below the minimum (cuticular) value.
Note that \(\theta\), \(\beta\) and \(Profit\) functions can be expressed as a function of stomatal conductance, instead of leaf water potential. This allows visualizing more clearly the effect of \(g_{sw,\min}\) and \(g_{sw,\max}\) thresholds on the maximum profit optimization strategy, as illustrated in the following figures.
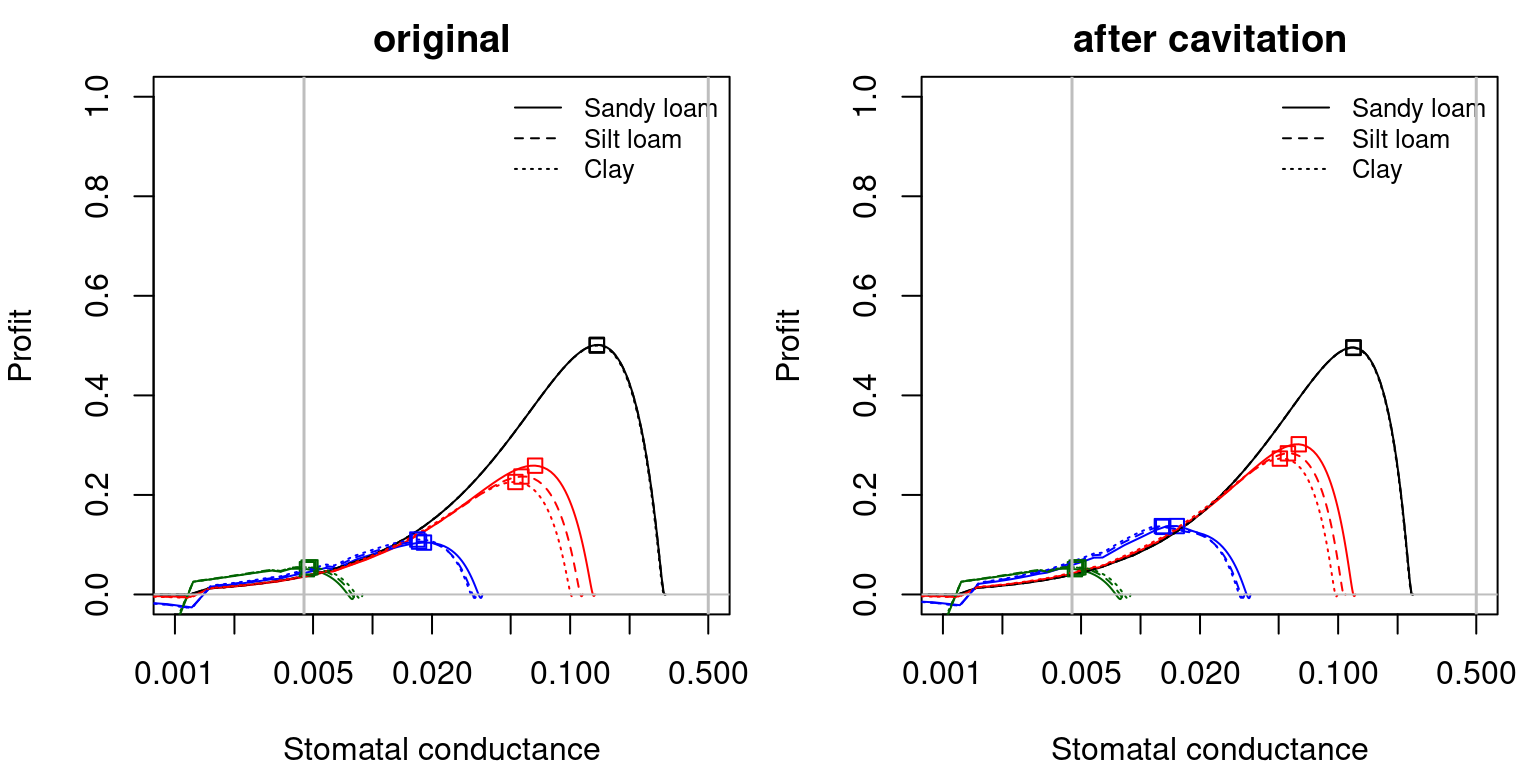
Figure 12.4: Profit function as a function of stomatal conductance, corresponding to fig. 12.3 and different soil textures and soil water potentials. Left/right panels show values for uncavitated/cavitated supply functions, respectively.
12.1.3 Cohort-level transpiration
In the previous section, we considered stomatal regulation at the leaf level only. At the plant cohort level, the gain function could be build from a crown photosynthesis function \(A(\Psi_{leaf})\), as shown in section 11.2. However, applying the profit maximization approach for a single crown photosynthesis function would imply the assumption that the same stomatal aperture occurs in all leaves of the plant cohort, independently of whether they are in shade or sunlit. A more realistic approach is to determine stomatal regulation by profit maximization for sunlit and shade leaves separately. The gain function and profit maximization calculations conducted for each leaf type yield instantaneous leaf water potentials \(\Psi^{sunlit}_{leaf}\) and \(\Psi^{shade}_{leaf}\) and instantaneous flow values \(E^{shade}\) and \(E^{sunlit}\) from the supply functions. The corresponding photosynthesis functions allow determining values for leaf temperatures \(T_{leaf}^{sunlit}\) and \(T_{leaf}^{shade}\), vapour pressure deficits \(VPD_{leaf}^{sunlit}\) \(VPD_{leaf}^{shade}\), stomatal conductance \(g_{sw}^{sunlit}\) and \(g_{sw}^{shade}\) and net photosynthesis rates \(A_{n}^{sunlit}\) and \(A_{n}^{shade}\). This is a lot of useful information at the leaf level for each plant cohort \(i\), but we also need transpiration and photosynthesis values at the plant cohort-level.
The average instantaneous flow rate (\(E_i^{average}\), in \(mmol\, H_2O \cdot s^{-1} \cdot m^{-2}\)) per leaf area unit of plant cohort \(i\) is the weighed average: \[\begin{equation} E_i^{average} = \frac{E_{i}^{shade} \cdot LAI_i^{sunlit} + E_{i}^{shade} \cdot LAI_i^{shade}}{LAI_i^{\phi}} \end{equation}\] where \(LAI_i^{sunlit}\) and \(LAI_i^{shade}\) are the cohorts LAI values for sunlit and shade leaves, from eq. (9.1), and \(LAI_i^{\phi}\) is the leaf area index of plant cohort \(i\). The model then uses the hydraulic supply function to find the transpiration rate \(E_i\) numerically closest to \(E_i^{average}\) (remember that the supply function is build in discrete steps). Finding the \(E_i\) value numerically closest to \(E_i^{average}\) determines the \(E_{i,t}\) the instantaneous transpiration flow for current time step \(t\), and also leads to setting values for \(t\) of several other variables, such as water potentials (\(\Psi_{leaf, i,t}\), \(\Psi_{stem, i,t}\), \(\Psi_{rootcrown, i,t}\), …), the slope of the supply function (\((d E/d\Psi_{i})_t\)), and instantaneous soil water extraction rates (\(E_{i,s,t}\)).
12.2 Stomatal regulation and transpiration under Cochard’s sub-model
12.2.1 Transpiration flows
In Sureau-ECOS (Ruffault et al. 2022), plants lose water through stomatal transpiration (\(E_{stom}\)), cuticular transpiration of the leaf (\(E_{leaf,cuti}\)) and cuticular transpiration of the stem (\(E_{stem, cuti}\)), see Fig. 10.2.
The total plant transpiration \(E_{Plant}\) is decomposed as the sum of the average leaf transpiration and wood cuticular transpiration: \[\begin{equation} E_{plant} = E_{leaf, average} + E_{stem, cuti} \end{equation}\] where \(E_{leaf, average}\) is computed as the weighted average of sunlit and shade leaf transpiration:
\[\begin{equation} E_{leaf, average} = \frac{E_{sunlit} \cdot LAI^{sunlit} + E_{leaf, shade} \cdot LAI^{shade}}{LAI^{\phi}} \end{equation}\]
In turn, \(E_{leaf, sunlit}\) and \(E_{leaf, shade}\) are the result of considering stomatal transpiration and cuticular transpiration: \[\begin{eqnarray} E_{leaf} &=& E_{stom} + E_{leaf, cuti} \\ &=& \left( \frac{1}{g_{stom} + g_{leaf, cuti}} + \frac{1}{g_{bound}}+ \frac{1}{g_{crown}}\right)^{-1} \cdot \frac{VPD_{leaf}}{P_{atm}} \end{eqnarray}\]
where \(VPD_{leaf}\) (in MPa) is the vapor pressure deficit of the leaf, \(P_{atm}\) is the atmospheric pressure, \(g_{stom}\) is the stomatal conductance, \(g_{leaf,cuti}\) is the cuticular conductance of the leaf, \(g_{bound}\) is the conductance of the leaf boundary layer and \(g_{crown}\) is the conductance of the tree crown. Note that sunlit and shade leaves will differ in \(g_{stom}\), \(g_{leaf,cuti}\) and \(VPD_{leaf}\), because of their different radiation and heat balance.
Finally, \(E_{stem, cuti}\) is calculated as follows: \[\begin{equation} E_{stem, cuti} = \left( \frac{1}{g_{stem, cuti}} + \frac{1}{g_{bound}}+ \frac{1}{g_{crown}}\right)^{-1} \cdot \frac{VPD_{air}}{P_{atm}} \end{equation}\] where \(VPD_{air}\) is the vapour pressure deficit in the canopy air: \[\begin{equation} VPD_{air} = e_{sat}(T_{air}) - e_{air} \end{equation}\]
12.2.2 Cuticular conductances
\(g_{leaf,cuti}\) is a function of leaf temperature (\(T_{leaf}\)), which is based on a single or double Q10 equation depending on whether leaf temperature is above or below the transition phase temperature (\(T_{phase}\)). If \(T_{leaf} \leq T_{phase}\) we have: \[\begin{equation} g_{leaf,cuti} = g_{leaf,cuti,20} \cdot Q_{10a}^{\frac{T_{leaf} - 20}{10}} \end{equation}\] whereas if \(T_{leaf} > T_{phase}\) we have: \[\begin{equation} g_{leaf,cuti} = g_{leaf,cuti,20} \cdot Q_{10a}^{\frac{T_{leaf} - 20}{10}} \cdot Q_{10b}^{\frac{T_{leaf} - T_{phase}}{10}} \end{equation}\]
Sunlit and shade leaves will have different \(g_{leaf,cuti}\) because of their different temperature. Unlike \(g_{leaf,cuti}\), \(g_{stem, cuti}\) is assumed non temperature dependent.
12.2.3 Stomatal conductance
\(g_{stom}\) is the stomatal conductance taking into account the dependence of stomata on light and temperature, as well as water status:
\[\begin{equation} g_{stom} = \lambda(\Psi_{leaf,sym}) · g_{stom, jarvis} \end{equation}\]
where \(g_{stom,jarvis}\) is the stomatal conductance without water stress and is determined as a function of light and temperature following Jarvis (1976). \(\lambda\) is a regulation factor that varies between 0 and 1 to represent stomatal closure according to leaf symplasmic water potential (\(\Psi_{leaf,sym}\)) using sigmoid-type function:
\[\begin{equation} \lambda(\Psi_{leaf,sym}) = 1 - \left(1 + e^{(slope_{gs}/25) \cdot (\Psi_{leaf,sym} - \Psi50_{gs}}) \right)^{-1} \end{equation}\]
depending on the potential at 50 % of stomatal closure (\(\Psi50_{gs}\)) and a shape parameter (\(slope_{gs}\)) describing the rate of decrease in stomatal conductance per unit of water potential drop.
With the current implementation, \(\lambda\) will be the same for sunlit and shade leaves (i.e. there is only one symplasmic water potential for both kind of leaves), but \(g_{stom, jarvis}\) will differ because of the different light and temperature conditions.
12.3 Cohort-level transpiration and photosynthesis
The amount of transpiration from the plant cohort in a given time step \(t\) (\(Tr_{i,t}\), in \(l \cdot m^{-2}\) of ground area, i.e. in mm) is: \[\begin{equation} Tr_{i,t} = E_{i,t} \cdot LAI_i^{\phi} \cdot 10^{-3} \cdot 0.01802 \cdot \Delta t_{step} \tag{12.1} \end{equation}\] where \(0.01802\) is the molar weight (in \(kg = l\)) of water and \(\Delta t_{step} = 86400/n_t\) the size of the time step in seconds, being \(n_t\) the number of time steps. Soil extraction rates (\(Ex\)) are scaled to the cohort level as done for transpiration: \[\begin{equation} Ex_{i,s,t} = E_{i,s,t} \cdot LAI_i^{\phi} \cdot 10^{-3} \cdot 0.01802 \cdot \Delta t_{step} \tag{12.2} \end{equation}\]
If plant capacitance is not considered, one should have that soil extraction equals transpiration: \[\begin{equation} Tr_{i,t} = Ex_{i,t} = \sum_s {Ex_{i,s,t}} \end{equation}\]
Instantaneous net photosynthesis per leaf area of sunlit and shade leaves in a given time step \(t\) (i.e. \(A_{n,i,t}^{sunlit}\) and \(A_{n,i,t}^{shade}\)) are also aggregated into \(A_{n,i,t}\), the net photosynthesis of the plant cohort \(i\) for the time step \(t\), in \(g\,C \cdot m^{-2}\) of ground area: \[\begin{equation} A_{n,i,t} = (A_{n,i,t}^{sunlit} \cdot LAI_i^{sunlit} + A_{n,i,t}^{shade} \cdot LAI_i^{shade}) \cdot 10^{-6} \cdot 12.01017 \cdot \Delta t_{step} \tag{12.3} \end{equation}\]
12.4 Cavitation and conduit refilling
Like with the basic water balance model, the advanced water balance model is normally run assuming that although soil drought may reduce transpiration. Embolized xylem conduits may be automatically refilled when soil moisture recovers if stemCavitationRecovery = "total". Automatic refilling is always assumed for root segments, but not for leaves and stems. There are three other options to deal with leaf and stem xylem cavitation besides automatic refilling. Any of them cause the model to keep track of the proportion of lost conductance in the leaf and stem xylem of the plant cohort \(i\) (\(PLC_{leaf,i}\) and \(PLC_{stem,i}\)) at successive time steps:
\[\begin{eqnarray}
PLC_{leaf,i, t} &=& \max \{PLC_{leaf,i, t-1}, 1 - k_{leaf,i}(\Psi_{leaf})/k_{max,leaf,i} \} \\
PLC_{stem,i, t} &=& \max \{PLC_{stem,i, t-1}, 1 - k_{stem,i}(\Psi_{stem})/k_{max,stem,i} \}
\end{eqnarray}\]
When water compartments are not considered, this equation is evaluated every hour time step, whereas it is evaluated every 1s with water compartments, as part of the constitutive equations (see ??).
For simulations of less than one year one can use stemCavitationRecovery = "none" to keep track of the maximum drought stress. However, for simulations of several years, it is normally advisable to allow recovery. If stemCavitationRecovery = "annual", \(PLC_{leaf,i}\) and \(PLC_{stem,i}\) values are set to zero at the beginning of each year, assuming that embolized plants overcome the conductance loss by creating new xylem tissue. Finally, if stemCavitationRecovery = "rate" the model simulates stem refilling at daily steps as a function of symplasmic water potential. First, a daily recovery rate (\(r_{refill}\); in \(cm^2 \cdot m^{-2} \cdot day^{-1}\)) is estimated as a function of \(\Psi_{symp,stem}\):
\[\begin{equation}
r_{refill}(\Psi_{symp,stem}) = r_{\max,refill} \cdot \max \{0.0, (\Psi_{symp,stem} + 1.5)/1.5\}
\end{equation}\]
Where \(r_{\max,refill}\) is the control parameter cavitationRecoveryMaximumRate indicating a maximum refill rate. The right part of the equation normalizes the water potential, so that \(r_{refill} = r_{refill,\max}\) if \(\Psi_{symp,stem} = 0\) and \(r_{refill} = 0\) if \(\Psi_{symp,stem} <= -1.5MPa\). The proportion of conductance lost in leaves and stem are then updated using:
\[\begin{eqnarray}
PLC_{leaf, i} &=& \max \{0.0, PLC_{leaf, i} - (r_{refill}/H_v) \} \\
PLC_{stem, i} &=& \max \{0.0, PLC_{stem, i} - (r_{refill}/H_v) \}
\end{eqnarray}\]
where \(H_v\) is the Huber value in units of \(cm^2 \cdot m^{-2}\).